题目内容
(本小题满分12分)
如图,用半径为R的圆铁皮,剪一个圆心角为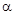 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角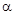 取什么值时,漏斗容积最大.(圆锥体积公式:
取什么值时,漏斗容积最大.(圆锥体积公式: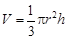 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)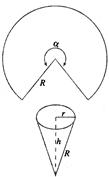
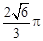
解析试题分析:设圆锥的底面半径为r,高为h,体积为V,那么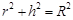 ,
,
因此,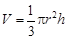 =
=
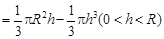 .………………………………(3分)
.………………………………(3分)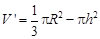 .
.
令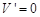 ,即
,即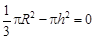 ,得
,得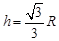 .…………………………………………(5分)
.…………………………………………(5分)
当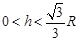 时,
时,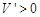 .
.
当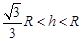 时,
时,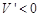 .
.
所以,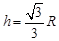 时,V取得极大值,并且这个极大值是最大值.……………………(8分)
时,V取得极大值,并且这个极大值是最大值.……………………(8分)
把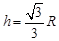 代入
代入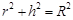 ,得
,得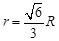 .
.
由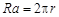 ,得
,得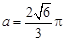
答:圆心角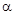 为
为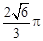 弧度时,漏斗容积最大.………………………………………(12分)
弧度时,漏斗容积最大.………………………………………(12分)
考点:函数导数求最值
点评:本题是函数应用题,首先找到容积与高或底面圆的半径间的函数关系式,进而通过导数工具求其最值

练习册系列答案
相关题目
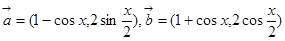 ,
,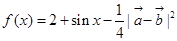 .
.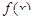 的表达式;
的表达式;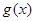 和函数
和函数 的图象关于原点对称,
的图象关于原点对称,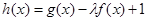 在区间
在区间 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围. 的最小正周期和最小值;
的最小正周期和最小值; 上的单调递增区间.
上的单调递增区间. 
 的图象过点
的图象过点 .
.  的值;
的值; 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, .若
.若 ,求
,求 的取值范围.
的取值范围. cosx (xÎR).
cosx (xÎR). )=
)= ,求cos2A的值.
,求cos2A的值.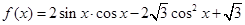 .
. 的值;
的值;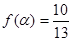 ,且
,且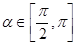 ,求
,求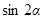 的值.
的值.
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 内角A,B,C的对边分别为
内角A,B,C的对边分别为 ,若向量
,若向量 共线,求
共线,求 的值。
的值。
 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;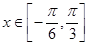 时,函数
时,函数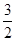 ,求不等式
,求不等式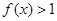 的解集.
的解集. ,
, .
. 的最大值;
的最大值; 中,角
中,角 、
、 的对边分别为
的对边分别为 、
、 ,若
,若 且
且 ,
, 的大小.
的大小.