题目内容
(理科)设离散型随机变量ξ可能取的值为1,2,3,4.P(ξ=k)=ak+b(k=1,2,3,4),又ξ的数学期望Eξ=3,则a+b等于
- A.

- B.

- C.

- D.

B
分析:根据随机变量ξ的分布列,写出四个变量对应的概率,并且根据概率之和是1得到关于a和b的方程,又有变量的期望值,列出关于a、b的另一个等式,进而结合两个方程解方程组即可得到答案.
解答:由题意可得:P(ξ=k)=ak+b(k=1,2,3,4),
∴P(ξ=1)+P(ξ=2)+P(ξ=3)+P(ξ=4)=(a+b)+(2a+b)+(3a+b)+(4a+b)=1,
整理得:10a+4b=1,…①
又因为ξ的数学期望Eξ=3,
所以(a+b)+2(2a+b)+3(3a+b)+4(4a+b)=3,
整理得:30a+10b=3,…②
由①②可得: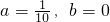 ,
,
所以a+b= .
.
故选B.
点评:解决此类问题的关键是熟练掌握离散型随机变量的分布列,以及其与期望之间的关系,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,是高考命题的热点之一.
分析:根据随机变量ξ的分布列,写出四个变量对应的概率,并且根据概率之和是1得到关于a和b的方程,又有变量的期望值,列出关于a、b的另一个等式,进而结合两个方程解方程组即可得到答案.
解答:由题意可得:P(ξ=k)=ak+b(k=1,2,3,4),
∴P(ξ=1)+P(ξ=2)+P(ξ=3)+P(ξ=4)=(a+b)+(2a+b)+(3a+b)+(4a+b)=1,
整理得:10a+4b=1,…①
又因为ξ的数学期望Eξ=3,
所以(a+b)+2(2a+b)+3(3a+b)+4(4a+b)=3,
整理得:30a+10b=3,…②
由①②可得:
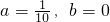 ,
,所以a+b=
 .
.故选B.
点评:解决此类问题的关键是熟练掌握离散型随机变量的分布列,以及其与期望之间的关系,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,是高考命题的热点之一.

练习册系列答案
相关题目