题目内容

已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
分析：先设出直线的参数方程，别代入椭圆、抛物线方程的到关于t的一元二次方程，设A、B、C、D的参数分别为t1、t2、t3、t4，利用根据与系数关系表示出|AB|：|CD|，从而得到所求．
解答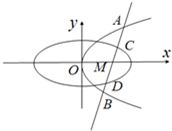：精英家教网解：设直线方程是
x=1+
1
2
t
y=
3
2
t
(t是参数)，分别代入椭圆、抛物线方程得：
5t2+4t-12=0（1）3t2-4pt-8p=0（2）
设A、B、C、D的参数分别为t1、t2、t3、t4，
则|AB|=|t1-t2|=
4
p2+6p
3
，|CD|=|t3-t4|=
16
5
，由|AB|：|CD|=5：3解得p=2．
点评：本题主要考查了直线与椭圆和抛物线之间的有关问题，求解圆锥曲线的综合题需画出图形理解题意，同时考查了直线的参数方程，以及参数方程的几何意义，属于中档题．
练习册系列答案
相关题目
已知椭圆C1：
x24
+y2=1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
（1）求椭圆C2的方程；
（2）设O为坐标原点，过O的直线l与C1相交于A，B两点，且l与C2相交于C，D两点．若|CD|=2|AB|，求直线l的方程．
已知椭圆C1：
x2
4
+y2=1，椭圆C2以椭圆C1的长轴为短轴，且与C1有相同的离心率，则椭圆C2的标准方程为
y2
16
+
x2
4
=1
y2
16
+
x2
4
=1
．
已知椭圆C1：
x2
4
+
y2
3
=1，其左准线为l1，右准线为l2，一条以原点为顶点，l1为准线的抛物线C2交l2于A，B两点，则|AB|等于（　　）
A、2B、4C、8D、16
如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网