题目内容
设t∈
R,m,n都是不为1的正数,函数f(x)=mx+t·nx.(
1)若m,n满足mn=1,请判断函数y=f(x)是否具有奇偶性.如果具有,求出相应的t的值;如果不具有,请说明理由;(
2)若m=2,n=
答案:
解析:
解析:
|
解:(1)因为 因为m,n都是不为1的正数,且 故当且仅当t=1时, (2)当 如果 于是有 所以函数 如果 于是有 所以函数 |

练习册系列答案
相关题目
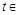 R,m,n都是不为1的正数,函数
R,m,n都是不为1的正数,函数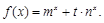
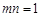 ,请判断函数
,请判断函数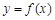 是否具有奇偶性. 如果具有,求出相
是否具有奇偶性. 如果具有,求出相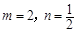 ,且
,且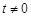 ,请判断函数
,请判断函数