题目内容
下列四个命题中可能成立的一个是
- A.
 ,且
,且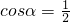
- B.sinα=0,且cosα=-1
- C.tanα=1,且cosα=-1
- D.α是第二象限角时,
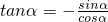
B
分析:由sin2α+cos2α=1 可得A不正确、B正确,根据tanα=1,可得 sinα=cosα= ,或sinα=cosα=-
,或sinα=cosα=- ,得C不正确,由tanα=
,得C不正确,由tanα= 可得D不正确.
可得D不正确.
解答:由sin2α+cos2α=1 可得A不正确、B正确.
根据tanα=1,可得 sinα=cosα= ,或sinα=cosα=-
,或sinα=cosα=- ,故C不正确.
,故C不正确.
由tanα= 可得D不正确.
可得D不正确.
故选B.
点评:本题主要考查同角三角函数的基本关系的应用,属于基础题.
分析:由sin2α+cos2α=1 可得A不正确、B正确,根据tanα=1,可得 sinα=cosα=
 ,或sinα=cosα=-
,或sinα=cosα=- ,得C不正确,由tanα=
,得C不正确,由tanα= 可得D不正确.
可得D不正确.解答:由sin2α+cos2α=1 可得A不正确、B正确.
根据tanα=1,可得 sinα=cosα=
 ,或sinα=cosα=-
,或sinα=cosα=- ,故C不正确.
,故C不正确.由tanα=
 可得D不正确.
可得D不正确.故选B.
点评:本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目