题目内容
(2012•辽宁)设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在[-
,
]上的零点个数为( )
| 1 |
| 2 |
| 3 |
| 2 |
分析:利用函数的奇偶性与函数的解析式,求出x∈[0,
],x∈[
,
]时,g(x)的解析式,推出f(0)=g(0),f(1)=g(1),g(
)=g(
)=0,画出函数的草图,判断零点的个数即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答: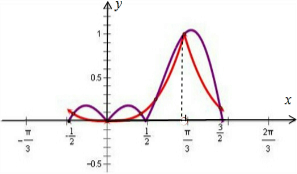 解:因为当x∈[0,1]时,f(x)=x3.
解:因为当x∈[0,1]时,f(x)=x3.
所以当x∈[1,2]时2-x∈[0,1],
f(x)=f(2-x)=(2-x)3,
当x∈[0,
]时,g(x)=xcos(πx);当x∈[
,
]时,g(x)=-xcosπx,
注意到函数f(x)、g(x)都是偶函数,
且f(0)=g(0),f(1)=g(1)=1,
g(
)=g(
)=0,
作出函数f(x)、g(x)的草图,
函数h(x)除了0、1这两个零点之外,
分别在区间[-
,0],[0,
],[
,1],[1,
]上各有一个零点.
共有6个零点,
故选B
 解:因为当x∈[0,1]时,f(x)=x3.
解:因为当x∈[0,1]时,f(x)=x3.所以当x∈[1,2]时2-x∈[0,1],
f(x)=f(2-x)=(2-x)3,
当x∈[0,
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
注意到函数f(x)、g(x)都是偶函数,
且f(0)=g(0),f(1)=g(1)=1,
g(
| 1 |
| 2 |
| 3 |
| 2 |
作出函数f(x)、g(x)的草图,
函数h(x)除了0、1这两个零点之外,
分别在区间[-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
共有6个零点,
故选B
点评:本题主要考查函数的奇偶性、对称性、函数的零点,考查转化能力、运算求解能力、推理论证能力以及分类讨论思想、数形结合思想,难度较大.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目