题目内容
已知集合U={(x,y)|x∈R,y∈R},M={(x,y)||x|+|y|<a},P={(x,y)y=f(x)},现给出下列函数:
①y=ax
②y=logax
③y=sin(x+a)
④y=cosax,
若0<a<1时,恒有P∩?uM=P,则f(x)所有可取的函数的编号是( )
①y=ax
②y=logax
③y=sin(x+a)
④y=cosax,
若0<a<1时,恒有P∩?uM=P,则f(x)所有可取的函数的编号是( )
| A、①②③④ | B、①②④ | C、①② | D、④ |
分析:利用补集的定义求出?uM,由P∩?uM=P,得到P⊆?uM,故P中的函数f(x)必须满足||x|+|y|≥a,检验各个选项是否满足此条件.
解答: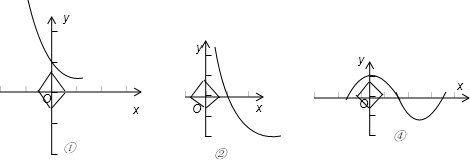 解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}⊆?uM,
解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}⊆?uM,
如图所示:结合图形可得满足条件的函数图象应位于曲线|x|+|y|=a(-a≤x≤a )的上方.
①中,x∈R,y>0,满足|x|+|y|≥a,故①可取.
②中,x>0,y=logax∈R,满足||x|+|y|≥a,故②可取.
③中的函数不满足条件,如 x=0,a=
时,y=
,不满足|x|+|y|≥a.
④中x∈R,-1≤y≤1,满足||x|+|y|≥a,故④可取.
故选B.
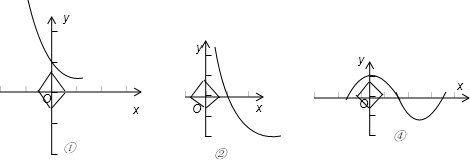 解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}⊆?uM,
解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}⊆?uM,如图所示:结合图形可得满足条件的函数图象应位于曲线|x|+|y|=a(-a≤x≤a )的上方.
①中,x∈R,y>0,满足|x|+|y|≥a,故①可取.
②中,x>0,y=logax∈R,满足||x|+|y|≥a,故②可取.
③中的函数不满足条件,如 x=0,a=
| π |
| 4 |
| ||
| 2 |
④中x∈R,-1≤y≤1,满足||x|+|y|≥a,故④可取.
故选B.
点评:本题考查补集的定义和运算,交集的定义和运算,求出?uM={(x,y)||x|+|y|≥a},是解题的关键.

练习册系列答案
相关题目
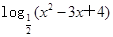 >-2且x∈Z},集合A={x|ax-1=0},集合B={x|
>-2且x∈Z},集合A={x|ax-1=0},集合B={x|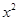 -(a+3)x+2a+2=0),若CUA=B,求a的值.
-(a+3)x+2a+2=0),若CUA=B,求a的值. UM=
.
UM=
.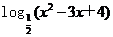 >-2且x∈Z},集合A={x|ax-1=0},集合B={x|
>-2且x∈Z},集合A={x|ax-1=0},集合B={x|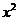 -(a+3)x+2a+2=0),若CUA=B,求a的值.
-(a+3)x+2a+2=0),若CUA=B,求a的值.