题目内容
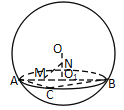
【题目】有一块三角形边角地,如图![]() ,
,![]() ,
,![]() ,
,![]() .(单位为百米).欲利用这块地修一个三角形形状的草坪(图中
.(单位为百米).欲利用这块地修一个三角形形状的草坪(图中![]() )供市民休闲,其中点
)供市民休闲,其中点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 的三边修建休闲长廊,规划部门要求
的三边修建休闲长廊,规划部门要求![]() 的面积占
的面积占![]() 面积的一半,设
面积的一半,设![]() (百米),
(百米),![]() 的周长为
的周长为![]() (百米)
(百米)

(1)求出![]() 函数的解析式及定义域
函数的解析式及定义域
(2)求出休闲长廊总长度![]() 的取值范围,并确定当
的取值范围,并确定当![]() 取到最大值时点
取到最大值时点![]() ,
,![]() 的位置
的位置
【答案】(1)![]() ,
,![]()
(2)![]() ,当
,当![]() 在
在![]() 处,点
处,点![]() 在线段
在线段![]() 的中点时最大值为
的中点时最大值为![]() 百米
百米
【解析】
(1)由![]() ,可先结合正弦定理的面积公式表示出
,可先结合正弦定理的面积公式表示出![]() ,再由余弦定理代换出
,再由余弦定理代换出![]() ,结合周长公式即可求解;
,结合周长公式即可求解;
(2)令![]() ,利用换元法和函数单调性即可求解
,利用换元法和函数单调性即可求解![]() 最值,以进一步确定点
最值,以进一步确定点![]() ,
,![]() 的位置
的位置
(1)设![]() ,
,![]() ,
,![]() ,
,![]()
由余弦定理可得![]() ,
,
即![]() ,则
,则![]() ,又
,又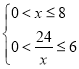 ,解得
,解得![]()
所以![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,
,
令![]() ,当且仅当
,当且仅当![]() 时,即
时,即![]() 时,
时,![]() ,
,
由对勾函数性质可知,当![]() 时
时![]() 单减,
单减,
当![]() 时,
时,![]() 单增,
单增,![]() ,
,![]() ,故
,故![]() ,
,
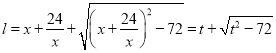 ,因为
,因为![]() ,故
,故![]() 整体单增,
整体单增,![]() 为增函数,故
为增函数,故![]() 时,
时,
![]() ,
,![]() 时,
时,![]() ,∴
,∴![]()
此时![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,则
,则![]() ,
,
![]() ,∴当
,∴当![]() 在
在![]() 处,点
处,点![]() 在线段
在线段![]() 的中点时最大值为
的中点时最大值为![]() 百米
百米

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
【题目】某公司为了促进某产品的销售,随机调查了该产品的月销售单价x(单位:元/件)及相应月销量y(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下数表:
的数据进行了统计,得到如下数表:
月销售单价 | 8 | 8.5 | 9 | 9.5 | 10 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该公司年底开展促销活动,当月销售单价为7元/件时,其月销售量达到14.8万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过0.5万件,则认为所得到的回归直线方程是理想的,试问(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
为何值时,公司月利润的预报值最大?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,
,![]()
参考数据:![]() ,
,![]()