题目内容
已知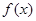 与
与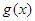 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且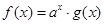
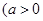 ,且
,且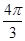 ,在有穷数列
,在有穷数列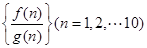 中,任意取前
中,任意取前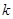 项相加,则前
项相加,则前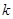 项和大于
项和大于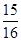 的概率是( )
的概率是( )
A.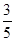 | B.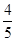 | C. | D. |
A
解析试题分析: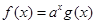 可知
可知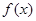 ,
, 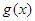 同号由
同号由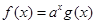 得
得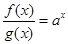
又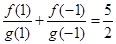 得
得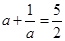
解得a=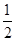 或a=2
或a=2
①a=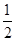 时,
时,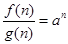 =
= 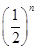 可知
可知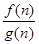 是以首项为
是以首项为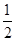 ,公比为
,公比为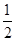 的等比数列,则前k项和为
的等比数列,则前k项和为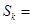
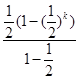 =
=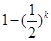 令
令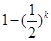 >
>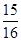 解得K="5" 所以前五项相加和才大于
解得K="5" 所以前五项相加和才大于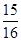
②a=2时,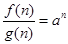 =
=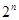 可知
可知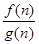 是以首项为2公比为2 的等比数列则前k项和
是以首项为2公比为2 的等比数列则前k项和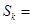
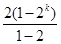 =
= 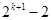 显然k="1" 时2>
显然k="1" 时2>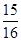 .
.
联立①②得概率为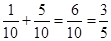 .故选A
.故选A
考点:1函数的导数.2.数列的知识.3.概率问题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
函数f(x)=1+x-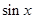 在(0,2π)上是( )
在(0,2π)上是( )
| A.增函数 | B.在(0,π)上递增,在(π,2π)上递减 |
| C.减函数 | D.在(0,π)上递减,在(0,2π)上递增 |
函数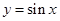 在点
在点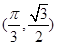 处的切线的斜率为( )
处的切线的斜率为( )
A. | B.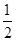 | C.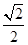 | D. |
已知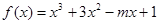 在
在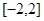 为单调增函数,则实数
为单调增函数,则实数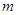 的取值范围为( )
的取值范围为( )
A.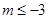 | B. | C.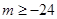 | D. |
设函数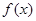 在R上存在导数
在R上存在导数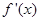 ,对任意的
,对任意的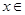 R,有
R,有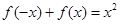 ,且
,且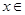 (0,+
(0,+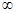 )时,
)时,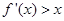 .若
.若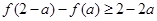 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
定积分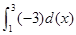 等于( )
等于( )
| A.-6 | B.6 | C.-3 | D.3 |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
 的导函数
的导函数 的图像如图所示,则
的图像如图所示,则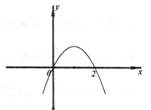
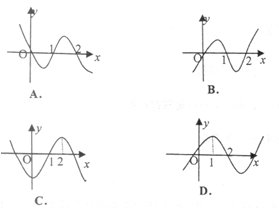
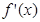 是函数
是函数 的导函数,将
的导函数,将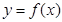 和
和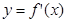 的图像画在同一个直角坐标系中,不可能正确的是( )
的图像画在同一个直角坐标系中,不可能正确的是( )