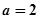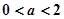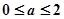题目内容
设平面区域D是由双曲线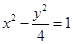 的两条渐近线和直线
的两条渐近线和直线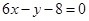 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当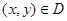 时,
时,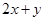 的最大值为( )
的最大值为( )
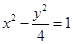 的两条渐近线和直线
的两条渐近线和直线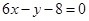 所围成三角形的边界及内部。当
所围成三角形的边界及内部。当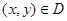 时,
时,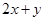 的最大值为( )
的最大值为( )| A.8 | B.0 | C.-2 | D.16 |
A
解:有平面区域D是由双曲线 x2-y2 /4 =1的两条渐近线和直线6x-y-8=0所围成三角形的边界及内部,所以得到区域为:

由于目标函数为2x+y,三角形的三个顶点坐标为(0,0),(1,-2),(2,4).
所求目标函数为2x+y的最大值为2×2+4=8

由于目标函数为2x+y,三角形的三个顶点坐标为(0,0),(1,-2),(2,4).
所求目标函数为2x+y的最大值为2×2+4=8

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
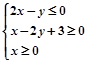 ,则
,则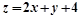 的最大值为
的最大值为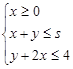 下,当
下,当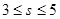 时,目标函数
时,目标函数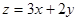 的最大值的变化范围是( )
的最大值的变化范围是( )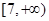
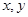 满足
满足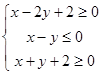 ,则
,则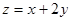 的最小值为__________
的最小值为__________
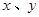 满足约束条件
满足约束条件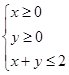 则
则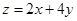 的最大值为 .
的最大值为 .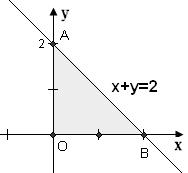
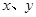 满足约束条件
满足约束条件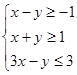 ,则目标函数
,则目标函数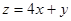 的最大值为( )
的最大值为( )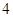

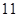
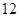
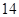
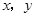 满足约束条件
满足约束条件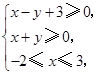 则目标函数
则目标函数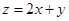 的最小值为( )
的最小值为( )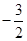 B. 12 C. 3 D. —3
B. 12 C. 3 D. —3 在直线
在直线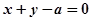 的同侧,则
的同侧,则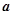 的取值范围是( )
的取值范围是( )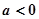 或
或
 或
或