题目内容
如图,已知A1B1C1-ABC是正三棱柱,D是AC中点.(1)证明AB1∥平面DBC1;
(2)假设AB1⊥BC1,BC=2,求线段AB1在侧面B1BCC1上的射影长.
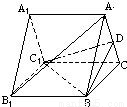
【答案】分析:(1)由A1B1C1-ABC是正三棱柱,可知四边形B1BCC1是矩形,连接B1C,交BC1于E,则B1E=EC.连接DE,由三角形中位线定理得到DE∥AB1,再由线面平行的判定定理得到结论.
(2)先作AF⊥BC,垂足为F.由面ABC⊥面B1BCC1,可知AF⊥B1BCC1平面B1F,由身影定义,可得B1F是AB1在平面B1BCC1内的射影.然后在矩形B1BCC1中,由△B1BF∽△BCC1求解.
解答: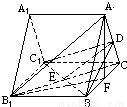 (1)证明:∵A1B1C1-ABC是正三棱柱,
(1)证明:∵A1B1C1-ABC是正三棱柱,
∴四边形B1BCC1是矩形.连接B1C,交BC1于E,则B1E=EC.连接DE.
在△AB1C中,∵AD=DC,∴DE∥AB1,又AB1?平面DBC1.DE?平面DBC1
∴AB1∥DBC1.(2)解:作AF⊥BC,垂足为F.
因为面ABC⊥面B1BCC1,所以AF⊥B1BCC1平面B1F.
连接B1F,则B1F是AB1在平面B1BCC1内的射影.
∵BC1⊥AB1,∴BC1⊥B1F.
∵四边形B1BCC1是矩形,∴∠B1BF=∠BCC1=90°;
∠FB1B=∠C1BC,∴△B1BF∽△BCC1.
∴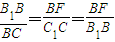
又F为正三角形ABC的BC边中点,因而B1B2=BF•BC=1×2=2,
于是B1F2=B1B2+BF2=3,∴B1F=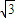 .
.
即线段AB1在平面B1BCC1内射影长为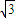
点评:本小题考查空间线面关系,正棱柱的性质,空间想象能力和逻辑推理能力.属中档题.
(2)先作AF⊥BC,垂足为F.由面ABC⊥面B1BCC1,可知AF⊥B1BCC1平面B1F,由身影定义,可得B1F是AB1在平面B1BCC1内的射影.然后在矩形B1BCC1中,由△B1BF∽△BCC1求解.
解答:
 (1)证明:∵A1B1C1-ABC是正三棱柱,
(1)证明:∵A1B1C1-ABC是正三棱柱,∴四边形B1BCC1是矩形.连接B1C,交BC1于E,则B1E=EC.连接DE.
在△AB1C中,∵AD=DC,∴DE∥AB1,又AB1?平面DBC1.DE?平面DBC1
∴AB1∥DBC1.(2)解:作AF⊥BC,垂足为F.
因为面ABC⊥面B1BCC1,所以AF⊥B1BCC1平面B1F.
连接B1F,则B1F是AB1在平面B1BCC1内的射影.
∵BC1⊥AB1,∴BC1⊥B1F.
∵四边形B1BCC1是矩形,∴∠B1BF=∠BCC1=90°;
∠FB1B=∠C1BC,∴△B1BF∽△BCC1.
∴
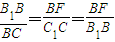
又F为正三角形ABC的BC边中点,因而B1B2=BF•BC=1×2=2,
于是B1F2=B1B2+BF2=3,∴B1F=
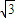 .
.即线段AB1在平面B1BCC1内射影长为
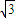
点评:本小题考查空间线面关系,正棱柱的性质,空间想象能力和逻辑推理能力.属中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
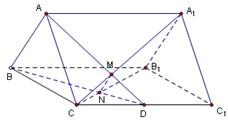 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,平面ABD和平面A1B1C的交线为MN. (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.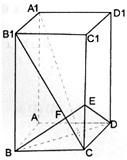 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.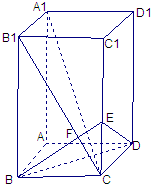 如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F