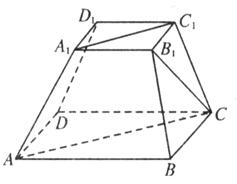
题目内容
已知正四棱台ABCD-A1B1C1D1的上底面?下底面周长分别为8和16,高为
(1)求上?下底面面积;
(2)求斜高及侧面积;
(3)求表面积.
| 3 |
(1)求上?下底面面积;
(2)求斜高及侧面积;
(3)求表面积.
分析:(1)根据正四棱台ABCD-A1B1C1D1的上底面?下底面是正方形,依据它们的周长求出边长,再求面积;
(2)在正四棱台ABCD-A1B1C1D1中,找出上、下底边心距
,
的差,高h,斜高h′构成一个直角三角形,用勾股定理求出斜高;
(3)利用表面积S表=S上底+S下底+S侧结合已知条件即可得出表面积.
(2)在正四棱台ABCD-A1B1C1D1中,找出上、下底边心距
| a |
| 2 |
| b |
| 2 |
(3)利用表面积S表=S上底+S下底+S侧结合已知条件即可得出表面积.
解答: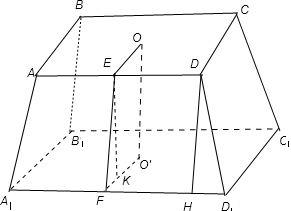 解:设上底的边长为a,下底的边长为b,斜高为h′.
解:设上底的边长为a,下底的边长为b,斜高为h′.
(1)∵4a=8,∴a=2,∴S上=a2=4,
∵4b=16,∴b=4,∴S下=b2=16.
故上?下底面面积分别为4,16.
(2)由于上、下底边心距
,
的差,高h,斜高h′构成一个直角三角形如右下图,
∴h′=
=
=2,即斜高为2.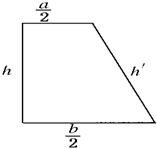
一个侧面面积=
×h′=6,
∴侧面积=4×6=24.
(3)S表=S上底+S下底+S侧=4+16+24=44,
即表面积为44.
 解:设上底的边长为a,下底的边长为b,斜高为h′.
解:设上底的边长为a,下底的边长为b,斜高为h′.(1)∵4a=8,∴a=2,∴S上=a2=4,
∵4b=16,∴b=4,∴S下=b2=16.
故上?下底面面积分别为4,16.
(2)由于上、下底边心距
| a |
| 2 |
| b |
| 2 |
∴h′=
h2+(
|
| 3+1 |

一个侧面面积=
| 2+4 |
| 2 |
∴侧面积=4×6=24.
(3)S表=S上底+S下底+S侧=4+16+24=44,
即表面积为44.
点评:本题考查棱台的结构特征、正四棱台的性质、棱柱、棱锥、棱台的体积,构造直角梯形和直角三角形,利用勾股定理是解决问题的关键.

练习册系列答案
相关题目
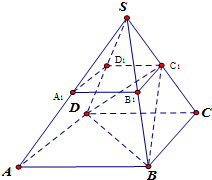 如图所示,正四棱台ABCD-A1B1C1D1是由一个正三棱锥S-ABCD(底面为正方形,顶点在底面上的射影为底面正方形的中心)被平行于底面的平面截所得.已知正四棱台ABCD-A1B1C1D1下底面边长为2,上底面边长为1,高为2.
如图所示,正四棱台ABCD-A1B1C1D1是由一个正三棱锥S-ABCD(底面为正方形,顶点在底面上的射影为底面正方形的中心)被平行于底面的平面截所得.已知正四棱台ABCD-A1B1C1D1下底面边长为2,上底面边长为1,高为2.