题目内容
设平面内两向量a与b互相垂直,且|a|=2,|b|=1,又k与t是两个不同时为零的实数.
(1)若x=a+(t-3)与y=-ka+tb垂直,求k关于t的函数关系式k=f(t);
(2)求函数k=f(t)的最小值.
答案:略
解析:
提示:
解析:
|
解:∵ x⊥y,∴a·b=0,又x⊥y,∴x·y=0,即[a+(t-3)b]·(-ka+tb)=0.
∵|a|=2,|b|=1, ∴ 即 (2)由(1)知, 即函数的最小值为 由已知条件知x⊥y,即x·y=0,可以得到函数关系式k=f(t),然后利用函数的性质求最值. |
提示:
|
本题体现了向量与二次函数的联系. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
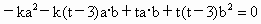 .
. .
.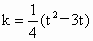 .
. ,
, .
. ,
, ,又k与t是两个不同时为零的实数.
,又k与t是两个不同时为零的实数. 与
与 垂直,求k关于t的函数关系式
垂直,求k关于t的函数关系式 ;
;