题目内容
例4.已知f(x)=ax2+bx+c,g(x)=ax+b(a、b、c∈R),当x∈[-1,1]时,|f(x)|≤1(1)证明:|c|≤1.
(2)x∈[-1,1]时,证明|g(x)|≤2.
(3)设a>0,当-1≤x≤1时,g(x)max=2,求f(x).
【答案】分析:(1)由f(0)=c,我们取x=0易得|c|=|f(0)|≤1
(2)有两种证法,证法一利用g(x)的单调性;证法二利用绝对值不等式||a|-|b||≤|a±b|≤|a|+|b|;
(3)a>0,g(x)在[-1,1]上是增函数,又由当-1≤x≤1时,g(x)max=2,即g(1)=a+b=f(1)-f(0)=2,结合x∈[-1,1]时,|f(x)|≤1,根据二次函数的性质,直线x=0为f(x)的图象的对称轴,进而出f(x)的解析式.
解答:证明:(1)由条件当=1≤x≤1时,|f(x)|≤1,
取x=0得|c|=|f(0)|≤1,即|c|≤1
(2)证法一:(利用函数的单调性)
由(1)得|c|≤1
当a>0时,g(x)=ax+b在[-1,1]上是增函数,
于是g(-1)≤g(x)≤g(1),(-1≤x≤1)
∵|f(x)|≤1,(-1≤x≤1),|c|≤1,
∴g(1)=a+b=f(1)-c≤|f(1)|+|c|=2,
g(-1)=-a+b=-f(-1)+c≥-(|f(-2)|+|c|)≥-2,
因此得|g(x)|≤2 (-1≤x≤1);
当a<0时,g(x)=ax+b在[-1,1]上是减函数,
于是g(-1)≥g(x)≥g(1),(-1≤x≤1),
∵|f(x)|≤1 (-1≤x≤1),|c|≤1
∴|g(x)|=|f(1)-c|≤|f(1)|+|c|≤2
综合以上结果,当-1≤x≤1时,都有|g(x)|≤2
证法二:(利用绝对值不等式的性质)
∵|f(x)|≤1(-1≤x≤1)
∴|f(-1)|≤1,|f(1)|≤1,|f(0)|≤1,
∵f(x)=ax2+bx+c,∴|a-b+c|≤1,|a+b+c|≤1,|c|≤1,
因此,根据绝对值不等式性质得
|a-b|=|(a-b+c)-c|≤|a-b+c|+|c|≤2,
|a+b|=|(a+b+c)-c|≤|a+b+c|+|c|≤2,
∵g(x)=ax+b,∴|g(±1)|=|±a+b|=|a±b|≤2,
函数g(x)=ax+b的图象是一条直线,
因此|g(x)|在[-1,1]上的最大值只能在区间的端点x=-1或x=1处取得,
于是由|g(±1)|≤2得|g(x)|≤2,(-1<x<1 )
解:(3)∵a>0,g(x)在[-1,1]上是增函数,
当x=1时取得最大值2,即g(1)=a+b=f(1)-f(0)=2…①
∵-1≤f(0)=f(1)-2≤1-2=-1,
∴c=f(0)=-1
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0),
根据二次函数的性质,直线x=0为f(x)的图象的对称轴,
由此得-<0,即b=0
由①得a=2,
∴f(x)=2x2-1
点评:本题主要考查二次函数的性质、含有绝对值不等式的性质,以及综合应用数学知识分析问题和解决问题的能力,二次函数的有关性质、函数的单调性是药引,而绝对值不等式的性质灵活运用是本题的灵魂,本题综合性较强,其解答的关键是对函数f(x)的单调性的深刻理解,以及对条件“-1≤x≤1时|f(x)|≤1”的运用;绝对值不等式的性质使用不当,会使解题过程空洞,缺乏严密,从而使题目陷于僵局.
(2)有两种证法,证法一利用g(x)的单调性;证法二利用绝对值不等式||a|-|b||≤|a±b|≤|a|+|b|;
(3)a>0,g(x)在[-1,1]上是增函数,又由当-1≤x≤1时,g(x)max=2,即g(1)=a+b=f(1)-f(0)=2,结合x∈[-1,1]时,|f(x)|≤1,根据二次函数的性质,直线x=0为f(x)的图象的对称轴,进而出f(x)的解析式.
解答:证明:(1)由条件当=1≤x≤1时,|f(x)|≤1,
取x=0得|c|=|f(0)|≤1,即|c|≤1
(2)证法一:(利用函数的单调性)
由(1)得|c|≤1
当a>0时,g(x)=ax+b在[-1,1]上是增函数,
于是g(-1)≤g(x)≤g(1),(-1≤x≤1)
∵|f(x)|≤1,(-1≤x≤1),|c|≤1,
∴g(1)=a+b=f(1)-c≤|f(1)|+|c|=2,
g(-1)=-a+b=-f(-1)+c≥-(|f(-2)|+|c|)≥-2,
因此得|g(x)|≤2 (-1≤x≤1);
当a<0时,g(x)=ax+b在[-1,1]上是减函数,
于是g(-1)≥g(x)≥g(1),(-1≤x≤1),
∵|f(x)|≤1 (-1≤x≤1),|c|≤1
∴|g(x)|=|f(1)-c|≤|f(1)|+|c|≤2
综合以上结果,当-1≤x≤1时,都有|g(x)|≤2
证法二:(利用绝对值不等式的性质)
∵|f(x)|≤1(-1≤x≤1)
∴|f(-1)|≤1,|f(1)|≤1,|f(0)|≤1,
∵f(x)=ax2+bx+c,∴|a-b+c|≤1,|a+b+c|≤1,|c|≤1,
因此,根据绝对值不等式性质得
|a-b|=|(a-b+c)-c|≤|a-b+c|+|c|≤2,
|a+b|=|(a+b+c)-c|≤|a+b+c|+|c|≤2,
∵g(x)=ax+b,∴|g(±1)|=|±a+b|=|a±b|≤2,
函数g(x)=ax+b的图象是一条直线,
因此|g(x)|在[-1,1]上的最大值只能在区间的端点x=-1或x=1处取得,
于是由|g(±1)|≤2得|g(x)|≤2,(-1<x<1 )
解:(3)∵a>0,g(x)在[-1,1]上是增函数,
当x=1时取得最大值2,即g(1)=a+b=f(1)-f(0)=2…①
∵-1≤f(0)=f(1)-2≤1-2=-1,
∴c=f(0)=-1
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0),
根据二次函数的性质,直线x=0为f(x)的图象的对称轴,
由此得-<0,即b=0
由①得a=2,
∴f(x)=2x2-1
点评:本题主要考查二次函数的性质、含有绝对值不等式的性质,以及综合应用数学知识分析问题和解决问题的能力,二次函数的有关性质、函数的单调性是药引,而绝对值不等式的性质灵活运用是本题的灵魂,本题综合性较强,其解答的关键是对函数f(x)的单调性的深刻理解,以及对条件“-1≤x≤1时|f(x)|≤1”的运用;绝对值不等式的性质使用不当,会使解题过程空洞,缺乏严密,从而使题目陷于僵局.

练习册系列答案
相关题目
 ,求f(x).
,求f(x). ,求f(x).
,求f(x). ,求f(x).
,求f(x).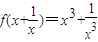 ,求f(x).
,求f(x).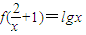 ,求f(x).
,求f(x).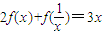 ,求f(x).
,求f(x).