题目内容
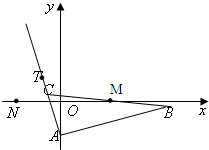 已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足| AT |
| AB |
(I)求AC边所在直线的方程;
(II)求△ABC的外接圆的方程;
(III)若点N的坐标为(-n,0),其中n为正整数.试讨论在△ABC的外接圆上是否存在点P,使得|PN|=|PT|成立?说明理由.
分析:(I)由已知中
•
=0可得AC⊥AB,结合T点坐标及AB的方程为x-3y-6=0点,我们易求出AC边所在直线的方程;
(II)结合(I)中结论,及B、C两点关于M点对称,可得△ABC的外接圆是以M为圆心,以BC为直径的圆,求出BC长即可得到圆的方程;
(III)若在△ABC的外接圆圆M上存在点P,使得|PN|=|PT|成立,则P为线段NT的垂直平分线L与圆M的公共点.所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P.由此设出N点坐标,代入点到直线距离公式进行验证,即可得到结论.
| AT |
| AB |
(II)结合(I)中结论,及B、C两点关于M点对称,可得△ABC的外接圆是以M为圆心,以BC为直径的圆,求出BC长即可得到圆的方程;
(III)若在△ABC的外接圆圆M上存在点P,使得|PN|=|PT|成立,则P为线段NT的垂直平分线L与圆M的公共点.所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P.由此设出N点坐标,代入点到直线距离公式进行验证,即可得到结论.
解答:解:(I)∵
•
=0∴AT⊥AB,又T在AC上∴AC⊥AB,△ABC为Rt△ABC,(1分)
又AB边所在直线的方程为x-3y-6=0,,所以直线AC的斜率为-3.(2分)
又因为点T(-1,1)在直线AC上,
所以AC边所在直线的方程为y-1=-3(x+1).即3x+y+2=0.(3分)
(II)AC与AB的交点为A,所以由
解得点A的坐标为(0,-2),(5分)
(6分)
又r=|AM|=
=2
.(7分)
从△ABC外接圆的方程为:(x-2)2+y2=8.(8分)
(III)若在△ABC的外接圆圆M上存在点P,使得|PN|=|PT|成立,则P为线段NT的垂直平分线L与圆M的公共点.所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P.
由N(-n,0),T(-1,1),知NT的斜率为
,线段NT的中点为(-
,
)
线段NT的垂直平分线L为y-
=-(n-1)(x+
)即2(1-n)x-2y+(2-n2)=0(10分)
圆M的圆心M到直线L的距离为
d=
=
(11分)
i)当n=1时,d=
,而r=2
,由d<r,此时直线L与圆M相交,存在满足条件的点P
ii)当n=2时d=
<
=r,此时直线L与圆M相交,存在满足条件的点P
iii)当n≥3时,d=
=
(
+
)>
•2
>
=r
此时直线L与圆M相离,不存在满足条件的点P.(14分)
| AT |
| AB |

又AB边所在直线的方程为x-3y-6=0,,所以直线AC的斜率为-3.(2分)
又因为点T(-1,1)在直线AC上,
所以AC边所在直线的方程为y-1=-3(x+1).即3x+y+2=0.(3分)
(II)AC与AB的交点为A,所以由
|
|
又r=|AM|=
| (2-0)2+(0+2)2 |
| 2 |
从△ABC外接圆的方程为:(x-2)2+y2=8.(8分)
(III)若在△ABC的外接圆圆M上存在点P,使得|PN|=|PT|成立,则P为线段NT的垂直平分线L与圆M的公共点.所以当L与圆M相离时,不存在满足条件的点P;当L与圆M相交或相切时则存在满足条件的点P.
由N(-n,0),T(-1,1),知NT的斜率为
| 1 |
| n-1 |
| n+1 |
| 2 |
| 1 |
| 2 |
线段NT的垂直平分线L为y-
| 1 |
| 2 |
| n+1 |
| 2 |
圆M的圆心M到直线L的距离为
d=
| |4(1-n)-0+2-n2| | ||
|
| |n2+4n-6| | ||
2
|
i)当n=1时,d=
| 1 |
| 2 |
| 2 |
ii)当n=2时d=
3
| ||
| 2 |
| 8 |
iii)当n≥3时,d=
| n2+4n-6 | ||
2
|
| 1 |
| 2 |
| n2-2n+2 |
| 6n-8 | ||
|
| 1 |
| 2 |
| 6n-8 |
| 8 |
此时直线L与圆M相离,不存在满足条件的点P.(14分)
点评:本题考查的知识点是直线与圆相交的性质,与直线关于点对称的直线方程,圆的标准方程,其中根据已知条件确定A,B,C三点的坐标及三边的关系,以判断三角形ABC的形状是解答本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
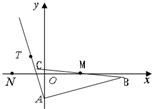 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足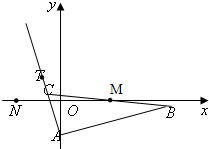 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
 (2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
(2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足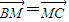 ,点T(-1,1)在AC边所在直线上且满足
,点T(-1,1)在AC边所在直线上且满足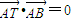 .
.