题目内容
在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c,如果acosB=bcosA,那么△ABC一定是
- A.锐角三角形
- B.钝角三角形
- C.直角三角形
- D.等腰三角形
D
分析:根据图形得,在直角△ACD和直角△BCD中,两次利用正弦定理得到bsinA=asinB,又因为bcosA=acosB,所以得到tanA=tanB,而∠A和∠B为锐角,所以∠A=∠B,所以三角形为等腰三角形.
解答: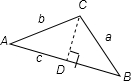
解法1:过C作CD⊥AB,垂足为D,
在直角△ACD中,根据正弦定理得: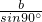 =
= ,
,
解得CD=bsinA,
在直角△BCD中,根据正弦定理得: =
=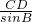 ,
,
解得CD=asinB,
所以bsinA=asinB,
又因为bcosA=acosB
两个等式联立得:tanA=tanB,
而∠A和∠B为锐角,所以∠A=∠B,
所以三角形为等腰三角形;
解法2:∵acosB=bcosA,
∴ =
=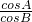 ,又根据正弦定理
,又根据正弦定理 =
= ,
,
∴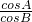 =
= ,即sinBcosA-sinAcosB=0,
,即sinBcosA-sinAcosB=0,
∴sin(B-A)=0,又A和B都为三角形的内角,
∴A=B,
即三角形为等腰三角形.
故选D
点评:考查学生利用正弦定理解决数学问题的能力,以及运用同角三角函数基本关系的能力.
分析:根据图形得,在直角△ACD和直角△BCD中,两次利用正弦定理得到bsinA=asinB,又因为bcosA=acosB,所以得到tanA=tanB,而∠A和∠B为锐角,所以∠A=∠B,所以三角形为等腰三角形.
解答:

解法1:过C作CD⊥AB,垂足为D,
在直角△ACD中,根据正弦定理得:
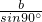 =
= ,
,解得CD=bsinA,
在直角△BCD中,根据正弦定理得:
 =
=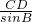 ,
,解得CD=asinB,
所以bsinA=asinB,
又因为bcosA=acosB
两个等式联立得:tanA=tanB,
而∠A和∠B为锐角,所以∠A=∠B,
所以三角形为等腰三角形;
解法2:∵acosB=bcosA,
∴
 =
=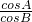 ,又根据正弦定理
,又根据正弦定理 =
= ,
,∴
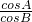 =
= ,即sinBcosA-sinAcosB=0,
,即sinBcosA-sinAcosB=0,∴sin(B-A)=0,又A和B都为三角形的内角,
∴A=B,
即三角形为等腰三角形.
故选D
点评:考查学生利用正弦定理解决数学问题的能力,以及运用同角三角函数基本关系的能力.

练习册系列答案
相关题目