题目内容
已知点A(1,2)在椭圆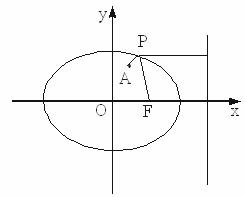
解:∵a2=16,b2=12,∴c2=4,c=2.
∴F为椭圆的右焦点,并且离心率为![]() =
=![]() .
.
设P到右准线的距离为d,则|PF|=![]() d, d=2|PF|.
d, d=2|PF|.
∴|PA|+2|PF|=|PA|+d.
由几何性质可知,当P点的纵坐标(横坐标大于零)与A点的纵坐标相同时,|PA|+d最小.
把y=2代入![]() =1,得x=
=1,得x=![]() (负舍),即P(
(负舍),即P(![]() ,2)为所求.
,2)为所求.
点评:由![]() 得d=2|PF|是求P点的关键.
得d=2|PF|是求P点的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
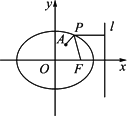
 对应变换下变为点B(1,2),求M-1.
对应变换下变为点B(1,2),求M-1.