题目内容
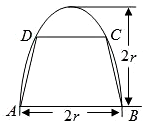 如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.(Ⅰ)求面积S以x为自变量的函数式,并写出其定义域;
(Ⅱ)求面积S的最大值.
分析:(I)依题意,以AB的中点O为原点建立直角坐标系,由图可得C的横坐标,进而可以表示出c的纵坐标,由解析式分析x的取值范围,即函数的定义域,可得答案;
(II)利用导数计算,记f(x)=4(x+r)2(r2-x2),(0<x<r),对其求导可得f′(x)=8(x+r)2(r-2x),求得其导函数的零点,分析其单调性,可得当x=
r时,S也取得最大值,即可得答案.
(II)利用导数计算,记f(x)=4(x+r)2(r2-x2),(0<x<r),对其求导可得f′(x)=8(x+r)2(r-2x),求得其导函数的零点,分析其单调性,可得当x=
| 1 |
| 2 |
解答: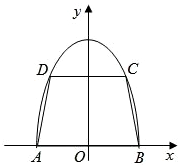 解:(I)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),
解:(I)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),
则点C的横坐标为x,
点C的纵坐标y满足方程
+
=1(y≥0),
解得y=2
(0<x<r)S=
(2x+2r)•2
=2(x+r)•
,
其定义域为{x|0<x<r}.
(II)记f(x)=4(x+r)2(r2-x2),(0<x<r),
则f′(x)=8(x+r)2(r-2x).
令f′(x)=0,得x=
r.
因为当0<x<
时,f′(x)>0;当
<x<r时,
f′(x)<0,所以f(
r)是f(x)的最大值.
因此,当x=
r时,S也取得最大值,最大值为
=
r2.
即梯形面积S的最大值为
r2.
 解:(I)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),
解:(I)依题意,以AB的中点O为原点建立直角坐标系O-xy(如图),则点C的横坐标为x,
点C的纵坐标y满足方程
| x2 |
| r2 |
| y2 |
| 4r2 |
解得y=2
| r2-x2 |
| 1 |
| 2 |
| r2-x2 |
=2(x+r)•
| r2-x2 |
其定义域为{x|0<x<r}.
(II)记f(x)=4(x+r)2(r2-x2),(0<x<r),
则f′(x)=8(x+r)2(r-2x).
令f′(x)=0,得x=
| 1 |
| 2 |
因为当0<x<
| r |
| 2 |
| r |
| 2 |
f′(x)<0,所以f(
| 1 |
| 2 |
因此,当x=
| 1 |
| 2 |
f(
|
3
| ||
| 2 |
即梯形面积S的最大值为
3
| ||
| 2 |
点评:本题考查椭圆方程及其性质的应用与根据导数求函数的最值的方法;第一注意结合题意,建立合适的坐标系,其次在运用导数求函数的最值时,注意自变量的实际意即函数的定义域.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
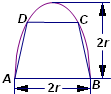 如图,有一块半椭圆形的钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,则梯形ABCD的面积S的最大值为
如图,有一块半椭圆形的钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,则梯形ABCD的面积S的最大值为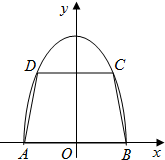 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.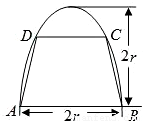 如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.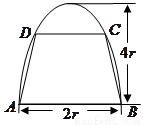 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为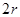 ,短半轴长为
,短半轴长为 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底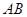 是半椭圆的短轴,上底
是半椭圆的短轴,上底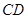 的端点在椭圆上,记
的端点在椭圆上,记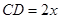 ,梯形面积为
,梯形面积为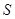 .
.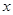 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;