题目内容
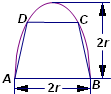 如图,有一块半椭圆形的钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,则梯形ABCD的面积S的最大值为
如图,有一块半椭圆形的钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,则梯形ABCD的面积S的最大值为分析:由题意可得椭圆的方程,求出其参数方程,然后由题意得出梯形的高与上底面的长度公式求出面积即可.
解答:解:以AB所在直线为 X轴,其垂直平分线为Y轴建系,则椭圆的参数方程为方程为x=rcosθ,y=2rsinθ,在图形中取AB中点O,连接OC,令角COB为θ
则下底边长为2r,上底边长为2rcosθ,高为2rsinθ,
故梯形的面积为S=
×2rsinθ=2r2(sinθ+sinθcosθ)
S′=2r2(2cos2θ+cosθ-1),令S′=0,得cosθ=
,故sinθ=
即当cosθ=
时,面积最大最大值为
r2
故答案为
r2
则下底边长为2r,上底边长为2rcosθ,高为2rsinθ,
故梯形的面积为S=
| 2r+2rcosθ |
| 2 |
S′=2r2(2cos2θ+cosθ-1),令S′=0,得cosθ=
| 1 |
| 2 |
| ||
| 2 |
即当cosθ=
| 1 |
| 2 |
3
| ||
| 2 |
故答案为
3
| ||
| 2 |
点评:本题考查根据实际问题选择函数类型,根据图形及题设本题选择了用椭圆的参数方程表示变量,给建立函数模型带来了方便,解题时要注意综合利用知识,尤其是在函数的应用题中,建立恰当的函数模型是求解的关键.

练习册系列答案
相关题目
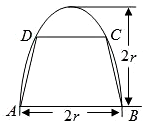 如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.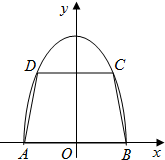 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.以AB为x轴,AB中点为原点建立平面直角坐标系.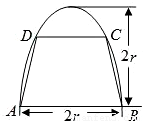 如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.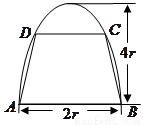 如图,有一块半椭圆形钢板,其半轴长为
如图,有一块半椭圆形钢板,其半轴长为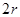 ,短半轴长为
,短半轴长为 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底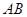 是半椭圆的短轴,上底
是半椭圆的短轴,上底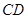 的端点在椭圆上,记
的端点在椭圆上,记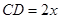 ,梯形面积为
,梯形面积为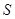 .
.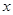 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;