题目内容
已知双曲线 上存在两点M,N关于直线y=x+m对称,且MN的中点在抛物线y2=9x上,则实数m的值为
上存在两点M,N关于直线y=x+m对称,且MN的中点在抛物线y2=9x上,则实数m的值为
- A.4
- B.-4
- C.0或4
- D.0或-4
D
分析:根据双曲线 上存在两点M,N关于直线y=x+m对称,求出MN中点P(-
上存在两点M,N关于直线y=x+m对称,求出MN中点P(- ,
, m),利用MN的中点在抛物线y2=9x上,即可求得实数m的值.
m),利用MN的中点在抛物线y2=9x上,即可求得实数m的值.
解答:∵MN关于y=x+m对称∴MN垂直直线y=x+m,MN的斜率-1,MN中点P(x0,x0+m)在y=x+m上,且在MN上
设直线MN:y=-x+b,∵P在MN上,∴x0+m=-x0+b,∴b=2x0+m
由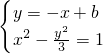 消元可得:2x2+2bx-b2-3=0
消元可得:2x2+2bx-b2-3=0
∴Mx+Nx=-b,∴x0=- ,∴b=
,∴b=
∴MN中点P(- ,
, m)
m)
∵MN的中点在抛物线y2=9x上,
∴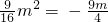
∴m=0-或4
故选D.
点评:本题考查直线与双曲线的位置关系,考查对称性,考查抛物线的标准方程,解题的关键是确定MN中点P的坐标.
分析:根据双曲线
 上存在两点M,N关于直线y=x+m对称,求出MN中点P(-
上存在两点M,N关于直线y=x+m对称,求出MN中点P(- ,
, m),利用MN的中点在抛物线y2=9x上,即可求得实数m的值.
m),利用MN的中点在抛物线y2=9x上,即可求得实数m的值.解答:∵MN关于y=x+m对称∴MN垂直直线y=x+m,MN的斜率-1,MN中点P(x0,x0+m)在y=x+m上,且在MN上
设直线MN:y=-x+b,∵P在MN上,∴x0+m=-x0+b,∴b=2x0+m
由
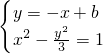 消元可得:2x2+2bx-b2-3=0
消元可得:2x2+2bx-b2-3=0 ∴Mx+Nx=-b,∴x0=-
 ,∴b=
,∴b=
∴MN中点P(-
 ,
, m)
m)∵MN的中点在抛物线y2=9x上,
∴
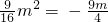
∴m=0-或4
故选D.
点评:本题考查直线与双曲线的位置关系,考查对称性,考查抛物线的标准方程,解题的关键是确定MN中点P的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
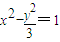 上存在两点M,N关于直线y=x+m对称,且MN的中点在抛物线y2=9x上,则实数m的值为( )
上存在两点M,N关于直线y=x+m对称,且MN的中点在抛物线y2=9x上,则实数m的值为( )