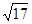题目内容
(本小题共14分)
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD= ,AP=
,AP= ,PC=
,PC= .
.

(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=
 ,AP=
,AP= ,PC=
,PC= .
.
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
(1)、(2)见解析;(3)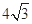 .
.
 .
.(18)解(Ⅰ)取PC的中点为O,连FO,DO,
∵F,O分别为BP,PC的中点,
∴ ∥BC,且
∥BC,且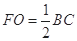 ,
,
又ABCD为平行四边形,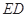 ∥BC,且
∥BC,且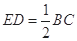 ,
,
∴ ∥ED,且
∥ED,且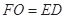
∴四边形EFOD是平行四边形 --------------------------------2分
即EF∥DO 又EF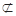 平面PDC
平面PDC
∴EF∥平面PDC. ------------------------------------------- 4分
(Ⅱ)若∠CDP=90°,则PD⊥DC,
又AD⊥平面PDC ∴AD⊥DP,
∴PD⊥平面ABCD, --------------------------------- 6分
∵BE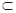 平面ABCD,
平面ABCD,
∴BE⊥DP -------------------------------- 8分
(Ⅲ)连结AC,由ABCD为平行四边形可知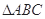 与
与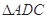 面积相等,
面积相等,
所以三棱锥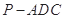 与三棱锥
与三棱锥 体积相等,
体积相等,
即五面体的体积为三棱锥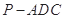 体积的二倍.
体积的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4
又∠CDP=120°PC=2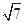 ,
,
由余弦定理并整理得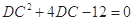 , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分
∴ 三棱锥
三棱锥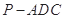 的体积
的体积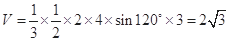
∴该五面体的体积为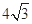 -------------------- 12分
-------------------- 12分
∵F,O分别为BP,PC的中点,
∴
 ∥BC,且
∥BC,且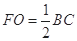 ,
,又ABCD为平行四边形,
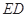 ∥BC,且
∥BC,且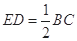 ,
,∴
 ∥ED,且
∥ED,且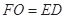
∴四边形EFOD是平行四边形 --------------------------------2分
即EF∥DO 又EF
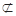 平面PDC
平面PDC ∴EF∥平面PDC. ------------------------------------------- 4分
(Ⅱ)若∠CDP=90°,则PD⊥DC,
又AD⊥平面PDC ∴AD⊥DP,
∴PD⊥平面ABCD, --------------------------------- 6分
∵BE
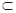 平面ABCD,
平面ABCD,∴BE⊥DP -------------------------------- 8分
(Ⅲ)连结AC,由ABCD为平行四边形可知
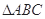 与
与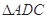 面积相等,
面积相等,所以三棱锥
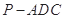 与三棱锥
与三棱锥 体积相等,
体积相等,即五面体的体积为三棱锥
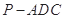 体积的二倍.
体积的二倍.∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4
又∠CDP=120°PC=2
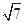 ,
,由余弦定理并整理得
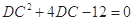 , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分∴
 三棱锥
三棱锥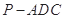 的体积
的体积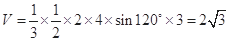
∴该五面体的体积为
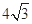 -------------------- 12分
-------------------- 12分
练习册系列答案
相关题目
 ;
; 的体积;
的体积; 

 的外接球
的外接球 的半径为
的半径为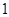 ,且满足
,且满足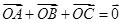 ,则正三棱锥
,则正三棱锥 的三视图如图所示,其中俯视图和侧视图都是腰长为
的三视图如图所示,其中俯视图和侧视图都是腰长为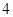 的等腰直角三角形,正视图为直角梯形.
的等腰直角三角形,正视图为直角梯形. ,求实数
,求实数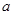 的值;
的值; ,求异面直线
,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;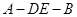 的平面角是
的平面角是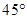 ,若存在,请求出
,若存在,请求出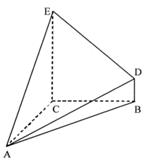


 ,OC=
,OC= ,则三棱锥O-ABC外接球的表面积为( )
,则三棱锥O-ABC外接球的表面积为( )



 ,则此圆柱的母线长为( )
,则此圆柱的母线长为( )