题目内容
（理）已知f（x）是定义在R上的不恒为零的函数，且对于任意非零的实数a，b∈R，满足f(a•b)=| f(b) |
| a |
| f(a) |
| b |
| 1 |
| 2 |
| f(2n) |
| n |
（1）f（1）=f（-1）； （2）f（x）为偶函数；
（3）数列{an}为等比数列； （4）数列{bn}为等差数列．
其中正确的是
分析：给a、b赋值，使它们都等于1，再使它们分别等于-1，1，得到结论（1）正确，把第三个条件两边同乘n化为整式形式，用第一个式子逐渐展开，得到等比数列，通过第二步整理，可得第三个结论正确．
解答：解：∵取a=b=1，可得f（1）=0，
取a=-1，b=1，可得f（-1）=0，
∴f（-1）=f（1），
即（1）正确，
∵f(a•b)=
+
，
∴f（2n）=f（2•2n-1）
=
+
=
+
=…
=
，
∴an=
，bn=n
∴（1），（3），（4）都正确，由已知不能判断函数的奇偶性，故（2）错误．
故答案为：（1），（3），（4）．
取a=-1，b=1，可得f（-1）=0，
∴f（-1）=f（1），
即（1）正确，
∵f(a•b)=
| f(b) |
| a |
| f(a) |
| b |
∴f（2n）=f（2•2n-1）
=
| f(2n-1) |
| 2 |
| f(2) |
| 2n-1 |
=
| f(2n-1) |
| 2 |
| 1 |
| 2n |
=…
=
| n |
| 2n |
∴an=
| 1 |
| 2n |
∴（1），（3），（4）都正确，由已知不能判断函数的奇偶性，故（2）错误．
故答案为：（1），（3），（4）．
点评：这种题做起来易出错，使学生系统掌握解等差数列与等比数列综合题的规律，深化数学思想方法在解题实践中的指导作用，灵活地运用数列知识和方法解决数学和实际生活中的有关问题
练习册系列答案
名校课堂系列答案
相关题目
，
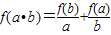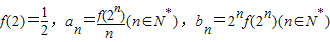，考查下列结论：