题目内容
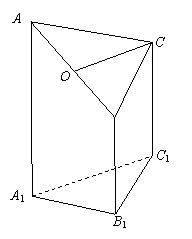 右图是一个直三棱柱(以
右图是一个直三棱柱(以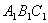 为底面)被
为底面)被
|
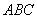 .
.
已知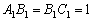 ,
, 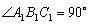 ,
,
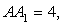
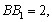
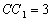 .
.
(Ⅰ)设点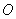 是
是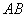 的中点,证明:
的中点,证明: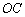 ∥平面
∥平面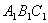 ;
;
(Ⅱ)求二面角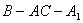 的大小.
的大小.
【答案】
解:法一:
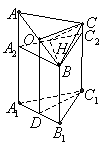 (Ⅰ)证明:作
(Ⅰ)证明:作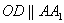 交
交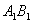 于
于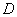 ,连
,连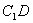 .……(1分)
.……(1分)
则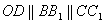 .
.
因为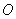 是
是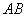 的中点,
的中点,
所以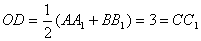 .
.
则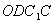 是平行四边形,因此有
是平行四边形,因此有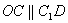 .……………………(3分)
.……………………(3分)
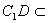 平面
平面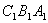 且
且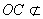 平面
平面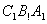 ,
,
则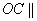 面
面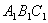 .
……………………(5分)
.
……………………(5分)
(Ⅱ)如图,过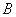 作截面
作截面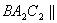 面
面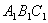 ,分别交
,分别交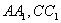 于
于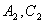 .
.
作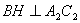 于
于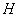 ,连
,连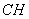 .
……………………(7分)
.
……………………(7分)
因为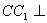 面
面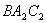 ,所以
,所以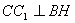 ,则
,则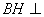 平面
平面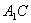 .
.
又因为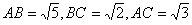
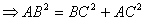 .
.
所以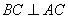 ,根据三垂线定理知
,根据三垂线定理知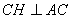 ,所以
,所以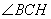 就是所求二面角的平面角.
就是所求二面角的平面角.
……………………(9分)
因为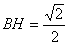 ,所以
,所以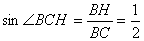 ,故
,故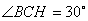 ,………(11分)
,………(11分)
即:所求二面角的大小为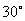 .
……………………(12分)
.
……………………(12分)
法二:
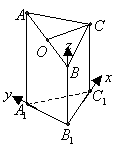 (Ⅰ)如图,以
(Ⅰ)如图,以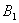 为原点建立空间直角坐标系, ………………(1分)
为原点建立空间直角坐标系, ………………(1分)
则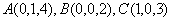
因为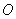 是
是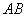 的中点,所以
的中点,所以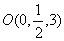 ,
,
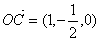 .
.
易知,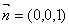 是平面
是平面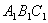 的一个法向量. ……(3分)
的一个法向量. ……(3分)
因为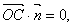
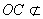 平面
平面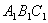 ,
,
所以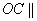 平面
平面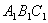 .
………………(5分)
.
………………(5分)
(Ⅱ)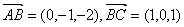 ,
,
设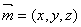 是平面
是平面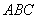 的一个法向量,则
的一个法向量,则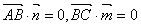 得:
得: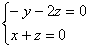
取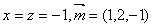 .
……………………(7分)
.
……………………(7分)
显然,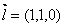 为平面
为平面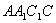 的一个法向量. ……………………(9分)
的一个法向量. ……………………(9分)
则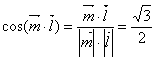 ,
……………………(11分)
,
……………………(11分)
结合图形可知所求二面角为锐角.
所以二面角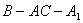 的大小是
的大小是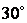 . ……………………(12分)
. ……………………(12分)

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3
右图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=900,AA1=4,BB1=2,CC1=3 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 .已知
.已知 ,
, ,
, ,
, ,
, .
.
 是
是 的中点,证明:
的中点,证明: 平面
平面 的大小;
的大小; 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为 已知
已知 ,
, ,
, ,
, ,
,

 是
是 的中点,证明:
的中点,证明: 平面
平面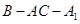 的大小;
的大小;