题目内容
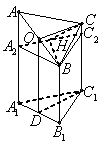
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以![]() 为底面)
为底面)
被一平面所截得到的几何体,截面为ABC.
已知![]() .
.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)证明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此几何体的体积.
解析:(1)证明:作![]() 交
交![]() 于
于![]() ,连
,连![]() .
.
则![]() .
.
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
则![]() 是平行四边形,因此有
是平行四边形,因此有![]() .
.
![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,
,
则![]() 面
面![]() .……………………………………4分
.……………………………………4分
(2)如图,过B作截面![]() 面
面![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() ,
,![]() .
.
作![]() 于
于![]() ,连
,连![]() .
.
因为![]() 面
面![]() ,所以
,所以![]() ,则
,则![]() 平面
平面![]() .
.
又因为![]() ,
,![]() ,
,![]() .
.
所以![]() ,根据三垂线定理知
,根据三垂线定理知![]() ,所以
,所以![]() 就是所求二面角的平面角.
就是所求二面角的平面角.
因为![]() ,所以
,所以![]() ,故
,故![]() ,
,
即:所求二面角的大小为![]() . ……………………………………………………9分
. ……………………………………………………9分
(3)因为![]() ,所以
,所以![]() .
.
![]() .
.
所求几何体体积为![]() . …………………………14分
. …………………………14分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
(本小题14分)执行右图中程序,回答下面问题。
|
(2)画出该程序的程序框图。
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以 平面
平面 ,
, ,且
,且 =2 .
=2 . 平面
平面 ;
;
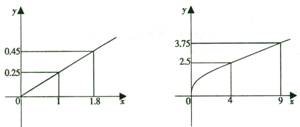
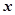 (万元)的函数关系式;
(万元)的函数关系式;