题目内容

（提示：请从以下两个不等式选择其中一个证明即可，若两题都答以第一题为准）
（1）设ai∈R+，bi∈R+，i=1，2，…n，且a1+a2+…an=b1+b2+…bn=2，求证：
a
2
1
a1+b1
+
a
2
2
a2+b2
+…+
a
2
n
an+bn
≥1
（2）设ai∈R+（i=1，2，…n），求证：
(a1+a2+…an)2
2(
a
2
1
+
a
2
2
+…
a
2
n
)
≤
a1
a2+a3
+
a2
a3+a4
+…+
an
a1+a2
．
分析：（1）欲证不等式的左式=(
a1+a2+…an+b1+b2+…bn
4
)(
a
2
1
a1+b1
+
a
2
2
a2+b2
+…
a
2
n
an+bn
)
=
1
4
[(a1+b1)+(a2+b2)+…+(an+bn)](
a
2
1
a1+b1
+
a
2
2
a2+b2
+…
a
2
n
an+bn
)结合柯西不等式即可得到证明．
（2）先由排序不等式，得：a12+a22+…+an2≥a1a2+a2a3+…+ana1，a12+a22+…+an2≥a1a3+a2a4+…+ana2两式相加后结合柯西不等式即可得到证明．
解答：证明：（1）左式=(
a1+a2+…an+b1+b2+…bn
4
)(
a
2
1
a1+b1
+
a
2
2
a2+b2
+…
a
2
n
an+bn
)
=
1
4
[(a1+b1)+(a2+b2)+…+(an+bn)](
a
2
1
a1+b1
+
a
2
2
a2+b2
+…
a
2
n
an+bn
)
≥
1
4
(
a1+b1
a1
a1+b1
+
a2+b2
a2
a2+b2
+…+
an+bn
an
an+bn
)2

=
1
4
(a1+a2+…an)2=1
（2）由排序不等式，得：a12+a22+…+an2≥a1a2+a2a3+…+ana1，a12+a22+…+an2≥a1a3+a2a4+…+ana2
两式相加：2（a12+a22+…+an2）≥a1（a2+a3）+a2（a3+a4）…+an（a1+a2），从而
2(
a
2
1
+
a
2
2
+…+
a
2
n
)(
a1
a2+a3
+
a2
a3+a4
+…+
an
a1+a2
)≥

≥（a1+a2+…an）2，即证．
点评：本小题主要考查不等式的证明、排序不等式、柯西不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
相关题目
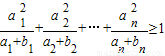
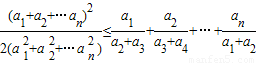（提示：请从以下两个不等式选择其中一个证明即可，若两题都答以第一题为准）
（1）设ai∈R+，bi∈R+，i=1，2，…n，且a1+a2+…an=b1+b2+…bn=2，求证：
（2）设ai∈R+（i=1，2，…n），求证：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网