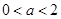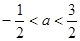题目内容
已知关于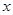 的方程
的方程 ,若
,若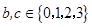 ,记“该方程有实数根
,记“该方程有实数根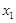 ,
,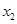 且满足
且满足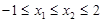 ”为事件A,则事件A发生的概率为( )
”为事件A,则事件A发生的概率为( )
A.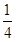 | B.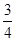 | C.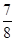 | D.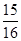 |
C
解析试题分析:要使得关于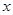 的方程
的方程 有实根,则满足
有实根,则满足 ,同时
,同时 ,
,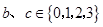 ,那么符合题意的所有情况为
,那么符合题意的所有情况为 ,而符合题意的情况.b=0,c=0,1,2;b=1,c=0,1,2,3;b=2,c=0,1,2,3;b=3,c=0,1,2,
,而符合题意的情况.b=0,c=0,1,2;b=1,c=0,1,2,3;b=2,c=0,1,2,3;b=3,c=0,1,2,
共有14种,那么根据古典概型概率公式可知事件A发生的概率选C.
考点:本试题主要是考查了古典概型的概率公式的运用。
点评:解决该试题的关键是能通过对于方程有实数根,满足的c,b的关系式,同时结合不等式的思想来得到符合题意的b,c的有序数对,确定出最大的基本事件空间,通过转化为古典概型来得到概率值。

练习册系列答案
相关题目
二次不等式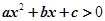 的解集是全体实数的条件是 ( )
的解集是全体实数的条件是 ( )
A.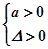 | B.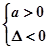 | C.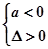 | D.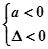 |
已知不等式 >0的解集为(-1,2),
>0的解集为(-1,2),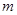 是
是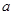 和
和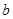 的等比中项,那么
的等比中项,那么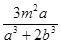 =
=
| A.3 | B.-3 | C.-1 | D.1 |
若定义在R上的函数f(x)满足 ,且
,且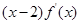 <0,a="f" (
<0,a="f" (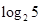 ),b="f" (
),b="f" (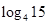 ),c="f" (
),c="f" ( ),则a,b,c的大小关系为
),则a,b,c的大小关系为
| A.a>b>c | B.c>b>a | C.b>a>c | D.c>a>b |
不等式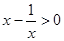 成立的充分不必要条件是( )
成立的充分不必要条件是( )
A.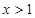 | B.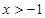 |
C.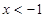 或 或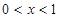 | D.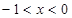 或 或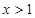 |
不等式- x -3 x -4>0的解集为 ( )
-3 x -4>0的解集为 ( )
A. | B. |
C. | D. |
在R上定义运算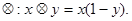 若对任意
若对任意 ,不等式
,不等式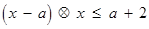 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是
A.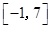 | B.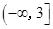 |
C.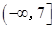 | D.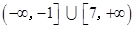 |
不等式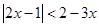 的解集为( )
的解集为( )
A.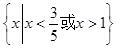 | B. |
C.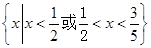 | D.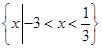 |
 :x
:x