题目内容
若数列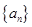 的前
的前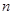 项和为
项和为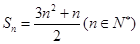 :;
:;
(Ⅰ) 求数列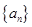 的通项公式
的通项公式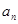 ;
;
(Ⅱ) 设数列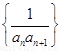 的前
的前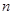 项和为
项和为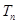 ,是否存在实数
,是否存在实数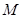 ,使得
,使得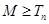 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出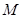 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
【答案】
【解析】本小题主要考查函数与数列的综合问题,考查等差数列通项公式,前项和公式,以及裂项求和,及放缩法证明不等式.
解:(Ⅰ)由题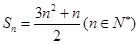
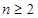 时
时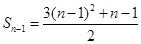 …………………………………………2分
…………………………………………2分
所以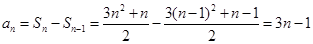 ,……………………5分
,……………………5分
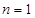 时
时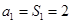 也适合上式, ………………………………………………………6分
也适合上式, ………………………………………………………6分
所以 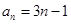
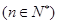 ………………………………………7分
………………………………………7分
(Ⅱ) 由(Ⅰ)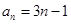
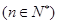
所以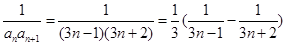 ……………………9分
……………………9分
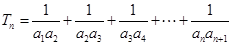
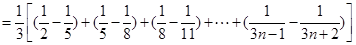 ……………………………………………10分
……………………………………………10分
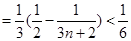 ……………………………………………12分
……………………………………………12分
使得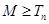 对一切正整数都成立,即
对一切正整数都成立,即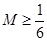 故存在
故存在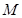 的最小值
的最小值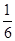 .…………………………………14分
.…………………………………14分

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 ,若数列
,若数列
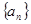 、
、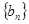 、
、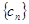 ,点
,点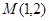 ,
,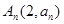 ,
,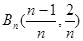 在一直线上。
在一直线上。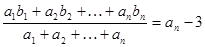 ,求数列
,求数列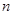 项和为
项和为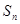 ,且满足
,且满足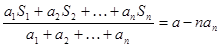 (
(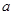 为常数),问点
为常数),问点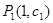 ,
,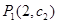 ,
, ,
,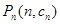 是否在同一直线上,请说明理由。
是否在同一直线上,请说明理由。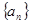 的前
的前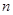 项和为
项和为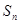 ,且满足
,且满足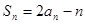 ,
,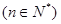 .
.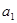 ,
,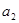 的值;
的值;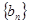 的前
的前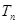 ,且满足
,且满足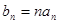
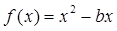 的图像在点
的图像在点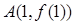 处的切线
处的切线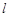 与直线
与直线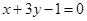 垂直,若数列
垂直,若数列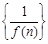 的前
的前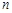 项和为
项和为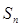 ,则
,则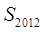 的值为( )
的值为( )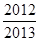 B.
B.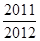 C.
C. 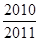 D.
D.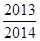
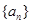 的前
的前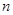 项和为
项和为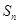 ,则
,则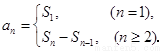
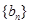 的前
的前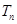 ,类比上述结果,则
,类比上述结果,则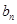 =_________;
=_________;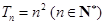 ,则
,则