Question

【题目】已知数列的前项和为，把满足条件的所有数列构成的集合记为.

（1）若数列通项为，求证：；

（2）若数列是等差数列，且，求的取值范围；

（3）若数列的各项均为正数，且，数列中是否存在无穷多项依次成等差数列，若存在，给出一个数列的通项；若不存在，说明理由.

Answer 1

【答案】（1）见解析；（2）；（3）数列中不存在无穷多项依次成等差数列.

【解析】

(1)由，得和，再证明，即可满足题意；（2）设的公差为，由，得，又，即，所以d=1，的取值范围；（3）假设数列中存在无穷多项依次成等差数列，不妨设该等差数列的第项为（为常数），由，得到当时，关于的不等式有无穷多个解，推出矛盾，所以不存在.

（1）因为，所以，所以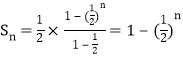 ，所以，即.

（2）设的公差为，因为，

所以

特别的当时，，即，

由得 ，整理得，因为上述不等式对一切恒成立，所以必有，解得，

又，所以，

于是，即，

所以，即，

所以，

因此的取值范围是.

（3）由得，所以，即，

所以，

从而有，

又，所以，即，

又，，

所以有，所以，

假设数列中存在无穷多项依次成等差数列，

不妨设该等差数列的第项为（为常数），

则存在，，使得，

即，

设，，，

则

即，

于是当时，，

从而有：当时，即，

于是当时，关于的不等式有无穷多个解，显然不成立，

因此数列中是不存在无穷多项依次成等差数列.