题目内容
经研究发现:平面内,半径为R的圆的内接矩形中,以正方形的周长为最大,最大值为4| 2 |
分析:平面类比到空间,圆对应球,正方形对应正方体,周长对应表面积,求最值时正方形的对角线是圆的直径,对应着正方体的体对角线这样就很快求出结果.
解答:解:平面圆类比空间的球体,那么平面中正方形类比空间正方体,长方形类比长方体等,正方形的对角线是圆的直径,对应着正方体的体对角线,所以正方体的边长为
,所以表面积为6× (
)2 =8R2故答案为正方体、8R2
| 2R | ||
|
| 2R | ||
|
点评:本题考查了类比推理,由平面推到空间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .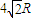 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .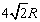 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 ▲ 的表面积为最大,最大值为 ▲ .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 ▲ 的表面积为最大,最大值为 ▲ .