Question

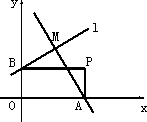
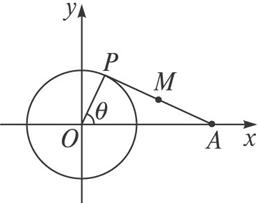
如图，点A是x轴上的动点，一条直线l经过点M(2，3)，且垂直于MA，并交y轴于点B．过A、B分别作x轴、y轴的垂线相交于点P，求点P的坐标(x，y)满足的关系．

Answer 1

答案：
解析：

解：如图，因为PA⊥x轴，点P的坐标为(x，y)，所以点A的坐标为(x，0)．因为PB⊥y轴，所以点B的坐标为(0，y)．由已知可得，MA所在直线的斜率kMA＝(x≠2)，MB所在直线的斜率kMB＝．因为MA⊥MB，所以kMA·kMB＝－1，即·＝－1(x≠2)，化简得2x＋3y－13＝0(x≠2)．当x＝2时，由题意知，点P与点M重合，即此时点P的坐标为(2，3)．又点P(2，3)满足方程2x＋3y－13＝0，所以点P的坐标(x，y)所满足的条件是2x＋3y－13＝0．