题目内容
若经过点P(0,2)且以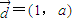 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .
【答案】分析:由题意可得,直线l的斜率为 a,故直线l的方程为 y-2=a(x-0),代入双曲线3x2-y2=1化简可得
(3-a2)x2-4ax-5=0,由题意可得 3-a2≠0,且 60-4a2>0,解不等式求得实数a的取值范围.
解答:解:由题意可得,直线l的斜率为 a,故直线l的方程为 y-2=a(x-0),代入双曲线3x2-y2=1化简可得
(3-a2)x2-4ax-5=0,由题意可得:3-a2≠0,且 60-4a2>0.
即 a≠±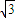 ,且-
,且-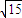 <a<
<a<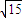 ,故实数a的取值范围是
,故实数a的取值范围是 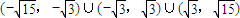 ,
,
故答案为: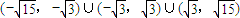 .
.
点评:本题考查直线和圆锥曲线的位置关系,得到 3-a2≠0,且 60-4a2>0,是解题的关键.
(3-a2)x2-4ax-5=0,由题意可得 3-a2≠0,且 60-4a2>0,解不等式求得实数a的取值范围.
解答:解:由题意可得,直线l的斜率为 a,故直线l的方程为 y-2=a(x-0),代入双曲线3x2-y2=1化简可得
(3-a2)x2-4ax-5=0,由题意可得:3-a2≠0,且 60-4a2>0.
即 a≠±
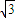 ,且-
,且-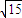 <a<
<a<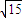 ,故实数a的取值范围是
,故实数a的取值范围是 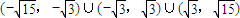 ,
,故答案为:
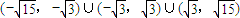 .
.点评:本题考查直线和圆锥曲线的位置关系,得到 3-a2≠0,且 60-4a2>0,是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 已知经过点P(0,2)且以
已知经过点P(0,2)且以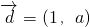 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是________.
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是________. 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .