题目内容
若经过点P(0,2)且以| d |
分析:由题意可得,直线l的斜率为 a,故直线l的方程为 y-2=a(x-0),代入双曲线3x2-y2=1化简可得
(3-a2)x2-4ax-5=0,由题意可得 3-a2≠0,且 60-4a2>0,解不等式求得实数a的取值范围.
(3-a2)x2-4ax-5=0,由题意可得 3-a2≠0,且 60-4a2>0,解不等式求得实数a的取值范围.
解答:解:由题意可得,直线l的斜率为 a,故直线l的方程为 y-2=a(x-0),代入双曲线3x2-y2=1化简可得
(3-a2)x2-4ax-5=0,由题意可得:3-a2≠0,且 60-4a2>0.
即 a≠±
,且-
<a<
,故实数a的取值范围是 (-
,-
)∪(-
,
)∪(
,
),
故答案为:(-
,-
)∪(-
,
)∪(
,
).
(3-a2)x2-4ax-5=0,由题意可得:3-a2≠0,且 60-4a2>0.
即 a≠±
| 3 |
| 15 |
| 15 |
| 15 |
| 3 |
| 3 |
| 3 |
| 3 |
| 15 |
故答案为:(-
| 15 |
| 3 |
| 3 |
| 3 |
| 3 |
| 15 |
点评:本题考查直线和圆锥曲线的位置关系,得到 3-a2≠0,且 60-4a2>0,是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 已知经过点P(0,2)且以
已知经过点P(0,2)且以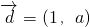 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是________.
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是________. 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .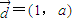 为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .
为方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B,则实数a的取值范围是 .