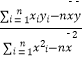题目内容
【题目】某钢厂打算租用
，
两种型号的火车车皮运输900吨钢材，
，
两种车皮的载货量分别为36吨和60吨，租金分别为1.6万元/个和2.4万元/个，钢厂要求租车皮总数不超过21个，且
型车皮不多于
型车皮7个，分别用
，
表示租用
，
两种车皮的个数.
（1）用
，
列出满足条件的数学关系式，并画出相应的平面区域；
（2）分别租用
，
两种车皮的个数是多少时，才能使得租金最少？并求出此最小租金.
【答案】（1）见解析;（2）分别租用
、
两种车皮5个，12个时租金最小，且最小租金为36.8万元.
【解析】（1）由已知得
，
满足的数学关系式为
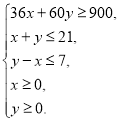
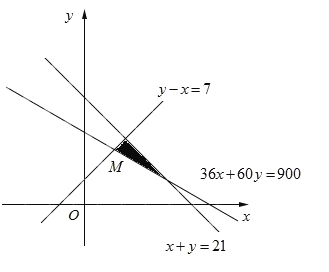
该二元一次不等式组所表示的平面区域为图中阴影部分所示.
（2）设租金为
元，则目标函数
，所以
，这是斜率为
，在
轴上的截距为
的一组平行直线.当
取最小值时，
的值最小，
又因为
，
满足约束条件，
所以由图可知，当直线
经过可行域中的点
时，截距
的值最小，即
的值最小.
解方程组
，得点
的坐标为
.
所以
（万元）.
答：分别租用
、
两种车皮5个，12个时租金最小，且最小租金为36.8万元.
练习册系列答案
阅读快车系列答案
相关题目
【题目】宿州市某登山爱好者为了解山高y（百米）与气温x（℃）之间的关系，随机统计了4次山高与相应的气温，并制作了对照表，由表中数据，得到线性回归方程为y=﹣2x+a，由此估计山高为72（百米）处的气温为（ ）
气温x（℃） | 18 | 13 | 10 | ﹣1 |
山高y（百米） | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4
