题目内容
已知P为椭圆
+
=1上一点，F1、F2是椭圆的两个焦点，∠F1PF2=60°，求△F1PF2的面积.
思路解析：本题集中了椭圆方程、三角形的面积、三角形的边角关系等条件，在这些条件中，都离不开|PF1|、|PF2|两条线段，由此可由椭圆的定义和三角形中的余弦定理出发，求得三角形的面积. 解：在椭圆 ∵点P在椭圆上，∴|PF1|+|PF2|=10. ① 由余弦定理,得|PF1|2+|PF2|2-2|PF1||PF2|cos60°=64. ② ①2-②得|PF1||PF2|=12,∴S=
+=1中，a=5，b=3，c=4.
|PF1||PF2|sin60°=
·12·
=3
.
练习册系列答案
完全考卷系列答案
同步课课练每课一练系列答案
新编教与学系列答案
课时同步配套练习系列答案
经纶学典提高班系列答案
普通高中新课程问题导学案系列答案
名牌牛皮卷提优名卷系列答案
海淀黄冈全程大考卷系列答案
金榜1卷通系列答案
相关题目
=1上的点，设F1，F2为椭圆的两个焦点，且∠F1PF2=
，求△F1PF2的面积.
+
=1上一点,P到一条准线的距离为P到相应焦点的距离之比为( )
B.
C.
D.
+
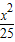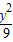=1上的点，F1、F2分别是椭圆的左、右焦点，若
=
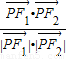，则△F1PF2的面积为（ ）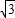
+
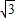
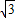
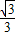
=1上的一点，F1、F2是该椭圆的两个焦点，若△PF1F2的内切圆半径为
，则
的值为（ ）
