题目内容
当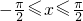
时，函数f（x）=sinx+
cosx的
- A.最大值是1，最小值是-1
- B.最大值是1，最小值是-
- C.最大值是2，最小值是-2
- D.最大值是2，最小值是-1
D
分析：首先对三角函数式变形，提出2变为符合两角和的正弦公式形式，根据自变量的范围求出括号内角的范围，根据正弦曲线得到函数的值域．
解答：∵f（x）=sinx+cosx
=2（sinx+
cosx）
=2sin（x+
），
∵
，
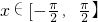∴f（x）∈[-1，2]，
故选D
点评：了解各公式间的内在联系，熟练地掌握这些公式的正用、逆用以及某些公式变形后的应用．掌握两角和与差的正弦、余弦、正切公式及其推导，本题主要是公式的逆用和对三角函数值域的考查．
分析：首先对三角函数式变形，提出2变为符合两角和的正弦公式形式，根据自变量的范围求出括号内角的范围，根据正弦曲线得到函数的值域．
解答：∵f（x）=sinx+
cosx=2（
sinx+cosx）=2sin（x+
），∵
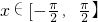，∴f（x）∈[-1，2]，
故选D
点评：了解各公式间的内在联系，熟练地掌握这些公式的正用、逆用以及某些公式变形后的应用．掌握两角和与差的正弦、余弦、正切公式及其推导，本题主要是公式的逆用和对三角函数值域的考查．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
．
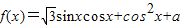时，函数f（x）的最大值与最小值的和为
，求a的值．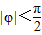
．
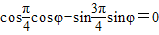，求φ的值；
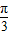，求当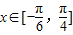
时，函数f（x）的值域．
定义在区间
上的函数y=f（x）的图象关于直线
对称，当
时，函数f（x）=Asin（ωx+φ），
，其图象如图．
上的表达式；
的解集．
时，函数f（x）=Asin（x+φ）（A＞0）取得最小值，则函数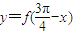
是（ ）
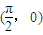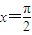对称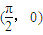
对称
对称
函数
时,求函数f（x）的值域．