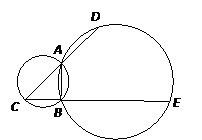题目内容
如图，A，B是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC=4，BE=10，且BC=AD，则AB=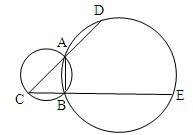
分析：根据割线定理得CA×CD=CB×CE，从而可求得PC的长，也就不难求得AB的长．
解答：解：设BC=x，由割线定理，
得CA×CD=CB×CE，即4（4+x）=x（x+10）．
解得x=2，因为AC是小圆的直径，
则AB=
=2
．
故填：2
．
得CA×CD=CB×CE，即4（4+x）=x（x+10）．
解得x=2，因为AC是小圆的直径，
则AB=
| AC2-BC2 |
| 3 |
故填：2
| 3 |
点评：此题主要是考查与圆有关的比例线段，运用了切线长定理，注意最后利用AC是小圆的直径构成的直角三角形求解．
练习册系列答案
相关题目
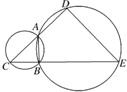
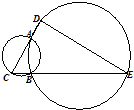（几何证明选讲选做题） 如图，A、B是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC=4，BE=10，且BC=AD，则DE=