题目内容
(本小题满分12分)
已知 ,写出用
,写出用 表示
表示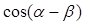 的关系等式,并证明这个关系等式.
的关系等式,并证明这个关系等式.

解析试题分析:如图,在平面直角坐标系
xoy内作单位圆O,以Ox为始边作角 ,它们的终边与单位圆的交点分别
,它们的终边与单位圆的交点分别
为A,B.
则  ,
, .
.
由向量数量积的定义,有 .
.
由向量数量积的的坐标表示,有

于是
 . ①------7分
. ①------7分
对于任意的 ,总可选取适当的整数k,使得
,总可选取适当的整数k,使得 =
= +
+ 或
或 =-
=- +
+ 成立.
成立.
故对于任意的 ,总有
,总有 成立,带入①式得
成立,带入①式得
对 ,总有
,总有 成立.------12分
成立.------12分
另证:由于 都是任意角,
都是任意角, 也是任意角.由诱导公式,总可以找到一个角
也是任意角.由诱导公式,总可以找到一个角 .
.
当  时,
时, ,则有
,则有 ,带入①既得
,带入①既得 .
.
当 时,
时, ,
, 就是
就是 的夹角
的夹角 ,则有
,则有 ,带入①既得
,带入①既得 .
.
综上,对 ,总有
,总有 .------12分
.------12分
考点:利用向量证明两角差的余弦展开式
点评:向量在高中数学的多个板块应用广泛,如向量解三角形求内角,向量表示直线间的垂直平行关系,向量证明立体几何中的线面的垂直平行关系及求异面直线所成角,线面角及二面角等

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设锐角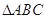 的三内角
的三内角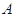 、
、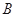 、
、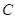 所对边的边长分别为
所对边的边长分别为 、
、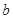 、
、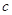 ,且
,且 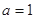 ,
,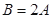 ,则
,则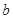 的取值范围为( )
的取值范围为( )
A.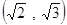 | B.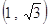 | C.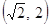 | D. |
 ,且当
,且当 时,
时, 的最小值为2.
的最小值为2. 的值,并求
的值,并求 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,再把所得图象向右平移
,再把所得图象向右平移 个单位,得到函数
个单位,得到函数 ,求方程
,求方程 在区间
在区间 上的所有根之和.
上的所有根之和. ⊥
⊥ .
.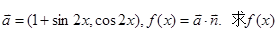 的最小正周期.
的最小正周期.  ,
,
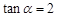 ,
, ,其中
,其中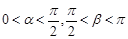 .
.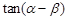 ;(2)求
;(2)求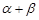 的值.
的值.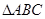 中,若
中,若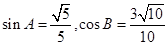 ,且
,且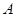 为锐角,求角
为锐角,求角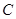 .
.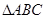 中,角
中,角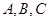 所对的边为
所对的边为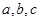 已知
已知 .
. 的值;
的值;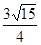 ,且
,且 ,求
,求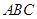 中,角
中,角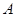 、
、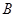 、
、 的对边分别为
的对边分别为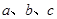 ,若
,若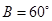 ,且
,且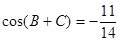 .
.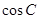 的值; (2)若
的值; (2)若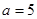 ,求△
,求△