题目内容
已知等差数列{an}中,a1=-4,且a1、a3、a2成等比数列,使{an}的前n项和Sn<0时,n的最大值为
- A.3
- B.4
- C.1
- D.2
A
分析:由题意可得,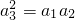 ,即
,即 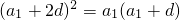 .把a1=-4 代入可得d=3,由Sn =-4n+
.把a1=-4 代入可得d=3,由Sn =-4n+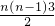 <0,求得正整数n的最大值.
<0,求得正整数n的最大值.
解答:∵等差数列{an}中,a1=-4,且a1、a3、a2成等比数列,
∴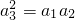 ,即
,即 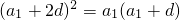 .
.
把a1=-4 代入可得d=3.
∴前n项和Sn =-4n+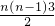 <0,解得 0<n<
<0,解得 0<n< ,n∈N.
,n∈N.
故n的最大值为3.
故选A.
点评:本题主要考查等比数列的定义和性质,等差数列的通项公式,前n项和公式及其应用,属于中档题.
分析:由题意可得,
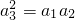 ,即
,即 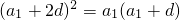 .把a1=-4 代入可得d=3,由Sn =-4n+
.把a1=-4 代入可得d=3,由Sn =-4n+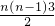 <0,求得正整数n的最大值.
<0,求得正整数n的最大值.解答:∵等差数列{an}中,a1=-4,且a1、a3、a2成等比数列,
∴
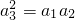 ,即
,即 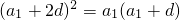 .
.把a1=-4 代入可得d=3.
∴前n项和Sn =-4n+
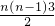 <0,解得 0<n<
<0,解得 0<n< ,n∈N.
,n∈N.故n的最大值为3.
故选A.
点评:本题主要考查等比数列的定义和性质,等差数列的通项公式,前n项和公式及其应用,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.