题目内容
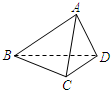
点E是正四面体ABCD的棱AD的中点,则异面直线BE与AC所成的角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:设F为CD边中点,连接EF,BF,根据三角形中位线定理,可得EF∥AC,即∠BEF即为异面直线BE与AC所成的角,解三角形BEF即可出异面直线BE与AC所成的角的余弦值
解答: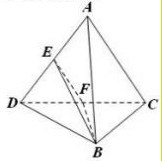 解:设F为CD边中点,连接EF,BF
解:设F为CD边中点,连接EF,BF
∵EF∥AC
∴∠BEF即为异面直线BE与AC所成的角
设正四面体的棱长为1,则EF=
AC=
,BF=BE=
∴cos∠BEF=
=
故选A
 解:设F为CD边中点,连接EF,BF
解:设F为CD边中点,连接EF,BF∵EF∥AC
∴∠BEF即为异面直线BE与AC所成的角
设正四面体的棱长为1,则EF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴cos∠BEF=
| BE2+EF2-BF2 |
| 2BE•EF |
| ||
| 6 |
故选A
点评:本题考查的知识点是异面直线及其所成的角,其中添加辅助线,构造异面直线夹角的平面角是解答,将异面直线夹角问题,转化为解三角形问题,是解答本题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
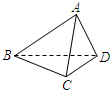 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.