题目内容
若在直线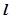 上存在不同的三个点
上存在不同的三个点 ,使得关于实数x的方程
,使得关于实数x的方程 有解(点
有解(点 不在
不在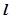 上),则此方程的解集为( )
上),则此方程的解集为( )
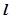 上存在不同的三个点
上存在不同的三个点 ,使得关于实数x的方程
,使得关于实数x的方程 有解(点
有解(点 不在
不在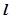 上),则此方程的解集为( )
上),则此方程的解集为( )A.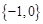 | B. | C. | D. |
D
利用向量的运算法则将等式中的向量都用以o为起点的向量表示,利用三点共线的条件列出方程求出x
解答:解:x2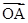 +x
+x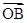 +
+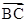 =
=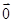
即x2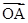 +x
+x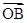 +
+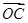 -
-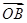 =
=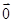
∴-x2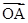 -x
-x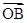 +
+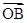 =
= 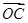
∵A,B,C共线
∴-x2-x+1=1解得x=0,-1
当x=0时,x2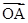 +x
+x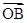 +
+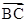 =
=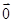 等价于
等价于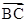 =
=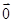 不合题意
不合题意
故选D.
解答:解:x2
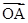 +x
+x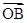 +
+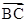 =
=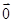
即x2
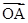 +x
+x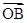 +
+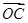 -
-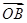 =
=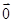
∴-x2
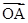 -x
-x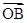 +
+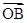 =
= 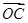
∴-x2-x+1=1解得x=0,-1
当x=0时,x2
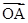 +x
+x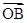 +
+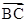 =
=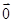 等价于
等价于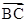 =
=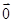 不合题意
不合题意
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 ,则
,则 ( )
( )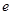



 ,
, ,
, ,则
,则 



 下表分段累计计算:
下表分段累计计算: )
) 元关于其当月工资
元关于其当月工资 元的函数
元的函数 (亿元)的关系有经验公式:
(亿元)的关系有经验公式: ,今该公司将3亿元投资这个项目,若设甲项目投资
,今该公司将3亿元投资这个项目,若设甲项目投资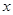 亿元,投资这两个项目所获得的总利润为
亿元,投资这两个项目所获得的总利润为 亿元.
亿元.
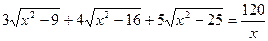 的解集______________
的解集______________ 的定义域是
的定义域是