题目内容
若z=mx+y在平面区域
上取得最小值时的最优解有无穷多个,则z的最小值是( )
|
分析:先有z=mx+y在平面区域
上取得最小值的最优解有无穷多个找出m=
.再把对应的平面区域画出,借助与图形找到此时z的最小值即可.
|
| 1 |
| 2 |
解答: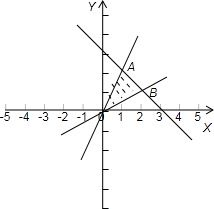 解:满足约束条件
解:满足约束条件
的平面区域如图示:
因为z=mx+y在平面区域上取得最小值的最优解有无穷多个,
所以m=
.
只有过点(0,0)时,z=mx+y有最小值0.
故选:C.
 解:满足约束条件
解:满足约束条件
|
因为z=mx+y在平面区域上取得最小值的最优解有无穷多个,
所以m=
| 1 |
| 2 |
只有过点(0,0)时,z=mx+y有最小值0.
故选:C.
点评:本题考查的知识点是简单线性规划的应用.在取得最值的最优解有无穷多个时,目标函数通常与线性约束条件中的某一条线平行.

练习册系列答案
相关题目
若z=mx+y在平面区域
上取得最小值的最优解有无穷多个,则z的最小值是( )
|
| A、-1 | B、0 | C、1 | D、0或±1 |
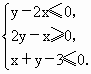 上取得最小值的最优解有无穷多个,则z的最小值是
上取得最小值的最优解有无穷多个,则z的最小值是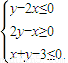 上取得最小值的最优解有无穷多个,则z的最小值是( )
上取得最小值的最优解有无穷多个,则z的最小值是( )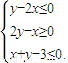 上取得最小值的最优解有无穷多个,则z的最小值是( )
上取得最小值的最优解有无穷多个,则z的最小值是( )