题目内容
在数列{an}中,已知a1=2,a2=3,当n≥2时,an+1是an•an﹣1的个位数,则a2010=
4
解析试题分析:由题意得,a3=a1•a2=6,a4=8,a5=8,a6=4,a7=2,a8=8,a9=6,a10=8,到此为止,看出一个周期,a9=a3,a10=a4,周期为6,利用这个周期能求出a2010.
由题意得,a3=a1•a2=6,定义f(x)=x的个位数
则a4=f(a3•a2)=8,
依此类推,a5=8,a6=4,a7=2,a8=8,a9=6,a10=8,
到此为止,看出一个周期,a9=a3,a10=a4,周期为6,
因为前2项不符合周期,所以2010﹣2=2008,2008=6×334+4,
所以a2010=a6=4.
故答案为:4.
考点:数列递推式
点评:本题考查数列的性质和应用,解题时要注意数列递推式的合理运用和周期性的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
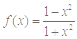 ,则
,则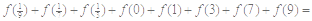 .
. 满足
满足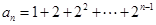 ,则
,则 项和
项和 = .
= . ,则
,则 =_____________。
=_____________。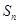 ,且
,且 ,则
,则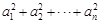 =___________
=___________ 满足
满足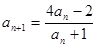 (
(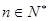 ).
).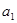 可以生成的数列
可以生成的数列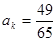 ”是“数列
”是“数列 为单调递增数列,则
为单调递增数列,则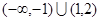 ;
;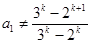 ,其中
,其中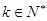 ,则
,则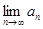 一定存在;
一定存在;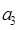 成等差数列.
成等差数列.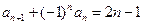 ,则{an}的前
,则{an}的前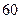 项和为
项和为