题目内容
给出下面的数表序列,其中表n(n=1,2,3 …)有n行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为an,例如a2=5,a3=17,a4=49.则:(1)a5=
(2)数列{an}的通项an=

分析:(1)根据图表可列出表4与表5,直接得到答案.
(2)先根据图象得到an=1+2×2+3×22+4×23+…+n×2n-1,再由错位相减法可求出an的表达式.
(2)先根据图象得到an=1+2×2+3×22+4×23+…+n×2n-1,再由错位相减法可求出an的表达式.
解答:解:(1)a5=129,
(2)依题意,an=1+2×2+3×22+4×23+…+n×2n-1①
由①×2得,2an=1×2+2×22+3×23+4×24+…+n×2n②
将①-②得-an=1+2+22+23+24+…+2n-1-n×2n=
-n×2n=2n-1-n×2n
所以an=(n-1)×2n+1.
故答案为:129,(n-1)×2n+1
(2)依题意,an=1+2×2+3×22+4×23+…+n×2n-1①
由①×2得,2an=1×2+2×22+3×23+4×24+…+n×2n②
将①-②得-an=1+2+22+23+24+…+2n-1-n×2n=
| 1(1-2n) |
| 1-2 |
所以an=(n-1)×2n+1.
故答案为:129,(n-1)×2n+1
点评:本题主要考查根据图象求出数列的项,考查数列的错位相减法.考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 给出下面的数表序列:其中表n(n=1,2,3…)有n行,第1行的n个数是1,3,5,…2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和.写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明).
给出下面的数表序列:其中表n(n=1,2,3…)有n行,第1行的n个数是1,3,5,…2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和.写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明). 的数表序列:
的数表序列: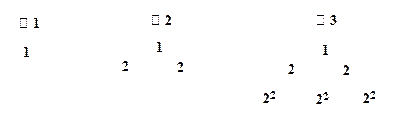
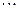 )有n行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为
)有n行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为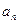 ,例如
,例如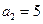 ,
,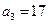 ,
, .则
.则 .
. 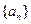 的通项
的通项