题目内容
若非空集合A={x|
>m,x∈Z}至多含有4个元素,则实数m的取值范围是
| 9-5x2 | ||
|
[2
-2,4+
)
| 2 |
| 5 |
[2
-2,4+
)
.| 2 |
| 5 |
分析:利用分母有理化,可将
>m(m∈Z)转化为
-2x>m(x∈Z),依题意:非空集合A={x|
-2x>m,x∈Z}至多含有4个元素即可求得实数m的取值范围.
| 9-5x2 | ||
|
| 9-x2 |
| 9-x2 |
解答:解:∵
=
=
=
-2x,
∴A={x|
>m,x∈Z}={x|
-2x>m,x∈Z};
∵9-x2≥0,
∴-3≤x≤3,又x∈Z,
∴x=-3,-2,-1,0,1,2,3;
令g(x)=
-2x,
则当x=-3时,g(-3)=6,
同理得g(-2)=4+
,g(-1)=2
+2,g(0)=3,g(1)=2
-2,g(2)=
-4,g(3)=-6,
将它们排列如下:
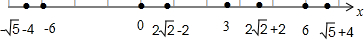
当m≥
+4时,A=∅,与非空集合A矛盾,不符合题意;
当m≥6时,A={-3},符合题意;
当m≥2
+2时,A={-2,-3},符合题意;
当m≥3时,A={-1,-2,-3},符合题意;
当m≥2
-2时,A={0,-1,-2,-3},符合题意;
∵非空集合A={x|
-2x>m,x∈Z}至多含有4个元素,
∴2
-2≤m<4+
.
∴实数m的取值范围是[2
-2,4+
).
| 9-5x2 | ||
|
(9-5x2)(
| ||||
(
|
(9-5x2)(
| ||
| (9-x2-4x2) |
| 9-x2 |
∴A={x|
| 9-5x2 | ||
|
| 9-x2 |
∵9-x2≥0,
∴-3≤x≤3,又x∈Z,
∴x=-3,-2,-1,0,1,2,3;
令g(x)=
| 9-x2 |
则当x=-3时,g(-3)=6,
同理得g(-2)=4+
| 5 |
| 2 |
| 2 |
| 5 |
将它们排列如下:
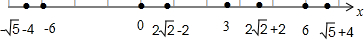
当m≥
| 5 |
当m≥6时,A={-3},符合题意;
当m≥2
| 2 |
当m≥3时,A={-1,-2,-3},符合题意;
当m≥2
| 2 |
∵非空集合A={x|
| 9-x2 |
∴2
| 2 |
| 5 |
∴实数m的取值范围是[2
| 2 |
| 5 |
点评:本题考查无理不等式的解法,着重考查分母有理化的应用,求得非空集合A={x|
-2x>m,x∈Z}是关键,也是难点,考查转化思想与分析运算能力,属于难题.
| 9-x2 |

练习册系列答案
相关题目
若非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则满足A∪B=B的所有a的集合是( )
| A、{a|1≤a≤9} | B、{a|6≤a≤9} | C、{a|a≤9} | D、∅ |