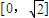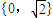Question

若P={y|y=x²，x∈R}，Q={y|y=x²+1，x∈R}，则P∩Q等于（　　）

A．P

B．Q

C．Φ

D．无法计算

Answer 1

分析：化简P={y|y≥0}，Q={y|y≥1}，利用两个集合的交集的定义求出P∩Q．

解答：解：∵P={y|y=x²，x∈R}={y|y≥0}，Q={y|y=x²+1，x∈R}={y|y≥1}，
∴P∩Q={y|y≥0}∩}{y|y≥1}={y|y≥1}=Q，
故选：B．

点评：本题主要考查集合的表示方法，两个集合的交集的定义和求法，属于基础题．