题目内容
设函数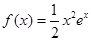 .
.
(1)求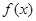 的单调区间;
的单调区间;
(2)若当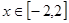 时,不等式
时,不等式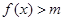 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
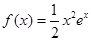 .
.(1)求
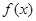 的单调区间;
的单调区间; (2)若当
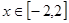 时,不等式
时,不等式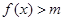 恒成立,求实数
恒成立,求实数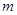 的取值范围.
的取值范围.(1)(-2,0)为?(x)减区间;(2)m<0.
本试题主要是考查了导数在研究函数中的运用。
解:(1)?′(x)=xex+ x2ex=
x2ex= x(x+2),
x(x+2),
令 x(x+2)>0,则x>0或x<-2, ∴(-∞,-2),(0,+ ∞)为?(x)的增区间.
x(x+2)>0,则x>0或x<-2, ∴(-∞,-2),(0,+ ∞)为?(x)的增区间.
令 x(x+2)<0,则-2<x<0, ∴(-2,0)为?(x)减区间.
x(x+2)<0,则-2<x<0, ∴(-2,0)为?(x)减区间.
(2)令?′(x)= xex+ x2e=
x2e= x(x+2)=0.
x(x+2)=0.
∴x=0和x=-2为极值点.
∵?(-2)=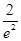 ,?(2)=2e2, ?(0)="0," ∴?(x)∈[0, 2e2]. ∴m<0
,?(2)=2e2, ?(0)="0," ∴?(x)∈[0, 2e2]. ∴m<0
解:(1)?′(x)=xex+
 x2ex=
x2ex= x(x+2),
x(x+2),令
 x(x+2)>0,则x>0或x<-2, ∴(-∞,-2),(0,+ ∞)为?(x)的增区间.
x(x+2)>0,则x>0或x<-2, ∴(-∞,-2),(0,+ ∞)为?(x)的增区间.令
 x(x+2)<0,则-2<x<0, ∴(-2,0)为?(x)减区间.
x(x+2)<0,则-2<x<0, ∴(-2,0)为?(x)减区间.(2)令?′(x)= xex+
 x2e=
x2e= x(x+2)=0.
x(x+2)=0.∴x=0和x=-2为极值点.
∵?(-2)=
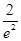 ,?(2)=2e2, ?(0)="0," ∴?(x)∈[0, 2e2]. ∴m<0
,?(2)=2e2, ?(0)="0," ∴?(x)∈[0, 2e2]. ∴m<0
练习册系列答案
相关题目
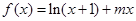 ,当
,当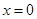 时,函数
时,函数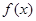 取得极大值.
取得极大值.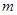 的值;
的值;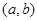 内导数都存在,且
内导数都存在,且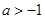 ,则存在
,则存在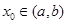 ,使得
,使得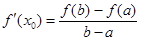 .试用这个结论证明:若
.试用这个结论证明:若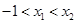 ,函数
,函数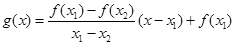 ,则对任意
,则对任意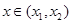 ,都有
,都有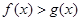 ;
;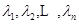 ,满足
,满足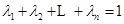 ,求证:当
,求证:当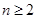 ,
,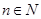 时,对任意大于
时,对任意大于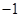 ,且互不相等的实数
,且互不相等的实数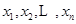 ,都有
,都有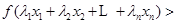
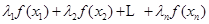 .
.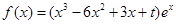 ,
, .
. 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围; ,使对任意的
,使对任意的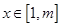 ,不等式
,不等式 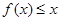 恒成立.求正整数
恒成立.求正整数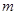 的最大值.
的最大值.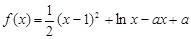 .
.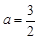 ,求函数
,求函数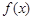 的极值;
的极值;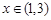 ,都有
,都有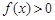 成立,求
成立,求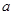 的取值范围.
的取值范围.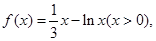 则
则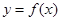 ( )
( )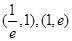 内均有零点。
内均有零点。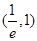 内有零点,在区间
内有零点,在区间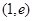 内无零点。
内无零点。 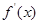 是
是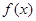 的导函数,
的导函数,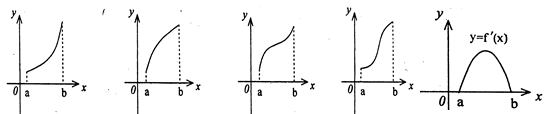

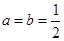 时,求函数
时,求函数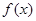 的最大值;
的最大值;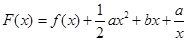 ,(
,(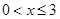 )其图象上任意一点
)其图象上任意一点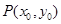 处切线的斜率
处切线的斜率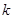 ≤
≤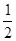 恒成立,求实数
恒成立,求实数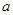 的取值范围;
的取值范围;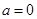 ,
,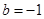 ,方程
,方程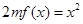 有唯一实数解,求正数
有唯一实数解,求正数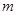 的值.
的值. ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.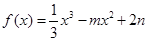 (
(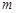 ,
,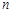 为常数),当
为常数),当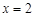 时,函数
时,函数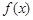 有极值,若函数
有极值,若函数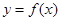 有且只有三个零点,则实数
有且只有三个零点,则实数