题目内容
如图,在正方体 中,E为AB的中点,F为
中,E为AB的中点,F为 的中点,求证:
的中点,求证:
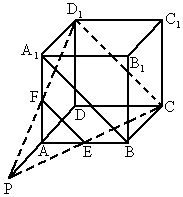
(1)E、C、 、F四点共面;
、F四点共面;
(2)CE、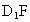 、DA三点共点.
、DA三点共点.
答案:略
解析:
解析:
|
证明:(1)分别连结EF、 ∵E、F分别是AB和 ∴ ∴四边 ∴ ∴ ∴E、F、 (2)∵ ∴直线 ∵ ∴ 又CE 即P是平面ABCD与平面 |

练习册系列答案
相关题目
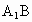 、
、 .
.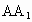 的中点,
的中点,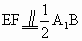 .又
.又 ,
,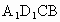 为平行四边形.
为平行四边形.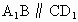 ,从而
,从而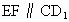 (见以下内容),
(见以下内容),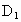 、C四点共面.
、C四点共面.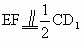 ,
,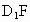 和CE必相交,设
和CE必相交,设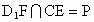 .
.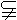 平面
平面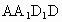 ,
,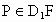 ,
, .
.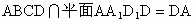 ,∴PÎ
DA,∴CE、
,∴PÎ
DA,∴CE、 中,E,F,G,H,M分别是棱
中,E,F,G,H,M分别是棱 ,
, ,
, 的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件________时,就有
的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件________时,就有 ;当N只需满足条件________时,就有MN∥平面
;当N只需满足条件________时,就有MN∥平面 .
.
 中,E、F分别是中点。
中,E、F分别是中点。 ;
; ;
;
 上是否存在点P使
上是否存在点P使 ,若存在,确定点P位置;若不存在,说明理由。
,若存在,确定点P位置;若不存在,说明理由。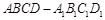 中,E、F、G分别为
中,E、F、G分别为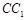 、
、 、
、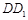 的中点,O为
的中点,O为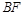 与
与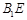 的交点,
的交点,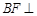 面
面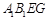
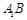 与平面
与平面 中,E、F、G、H分别为中点,则异面直线EF与GH所成的角等于( )
中,E、F、G、H分别为中点,则异面直线EF与GH所成的角等于( ) A.
A. B.
B. C.
C. D.
D.
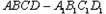 中,E、F分别是,
中,E、F分别是,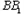 、CD的中点
、CD的中点 平面ADE.
平面ADE.