题目内容
(2012•郑州二模)为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,郑州市教育局举办了全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(I)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,199,试写出第二组第一位学生的编号;
(II) 求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在85.5?95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
| 分组 | 频数 | 频率 | |
| 一 | 60.5-70.5 | a | 0.26 |
| 二 | 70.5-80.5 | 15 | c |
| 三 | 80.5-90.5 | 18 | 0.36 |
| 四 | 90.5-100.5 | b | d |
| 合计 | 50 | e | |
(II) 求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在85.5?95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
分析:(I)根据系统抽样的特点可知将200个分组50组,每组4个,从而得到所求;
(Ⅱ)根据频数=样本容量×频率,频率=
可求出a,b,c,d,e的值,然后作出频率分布直方图即可;
(Ⅲ)先求出被抽到的学生中获二等奖的人数,然后计算该频率,从而可估计获二等奖的人数.
(Ⅱ)根据频数=样本容量×频率,频率=
| 频数 |
| 样本容量 |
(Ⅲ)先求出被抽到的学生中获二等奖的人数,然后计算该频率,从而可估计获二等奖的人数.
解答: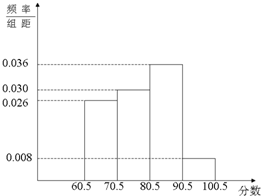 解:(Ⅰ)用系统抽样的方法抽取50个样本,将200个分组50组,每组4个,则第二组第一学生编号为004.…(3分)
解:(Ⅰ)用系统抽样的方法抽取50个样本,将200个分组50组,每组4个,则第二组第一学生编号为004.…(3分)
(Ⅱ)a=0.26×50=13,c=
=0.3,d=1-0.26-0.3-0.36=0.08,c=0.08×50=4,e=1
∴a,b,c,d,e的值分别为13,4,0.30,0.08,1,作出频率分布直方图…(8分)
(Ⅲ)在被抽到的学生中获二等奖的人数9+2=11(人),占样本的比例是
=0.22,
即获二等奖的概率为22%,所以获二等奖的人数估计为200×22%=44(人).
答:获二等奖的大约有44人.…(12分)
 解:(Ⅰ)用系统抽样的方法抽取50个样本,将200个分组50组,每组4个,则第二组第一学生编号为004.…(3分)
解:(Ⅰ)用系统抽样的方法抽取50个样本,将200个分组50组,每组4个,则第二组第一学生编号为004.…(3分)(Ⅱ)a=0.26×50=13,c=
| 15 |
| 50 |
∴a,b,c,d,e的值分别为13,4,0.30,0.08,1,作出频率分布直方图…(8分)
(Ⅲ)在被抽到的学生中获二等奖的人数9+2=11(人),占样本的比例是
| 11 |
| 50 |
即获二等奖的概率为22%,所以获二等奖的人数估计为200×22%=44(人).
答:获二等奖的大约有44人.…(12分)
点评:本题主要考查了频率分布直方图,以及系统抽样,同时考查了组图能力和运算求解的能力,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目