题目内容
已知向量 与
与 满足:|
满足:| |=4,|
|=4,| |=3,(2
|=3,(2 +3
+3 )•(2
)•(2 -
- )=61.
)=61.(Ⅰ)求
 •
• 的值;
的值;(Ⅱ)求向量
 与
与 的夹角;
的夹角;(Ⅲ)求|
 -
-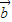 |的值.
|的值.
【答案】分析:(Ⅰ)由(2 +3
+3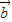 )•(2
)•(2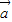 -
-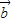 )=61得,4
)=61得,4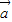 2+4
2+4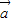 •
•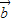 -3
-3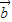 2=61将|
2=61将|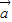 |=4,|
|=4,|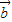 |=3,代入即可求得两向量的内积;
|=3,代入即可求得两向量的内积;
(Ⅱ)由公式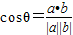 求出向量
求出向量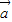 与
与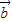 的夹角余弦,再由出对应的角;
的夹角余弦,再由出对应的角;
(Ⅲ)先求出(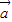 -
-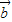 )2=
)2=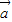 2-2
2-2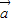 •
•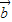 +
+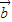 2=13,再开方求出两向量差的模.
2=13,再开方求出两向量差的模.
解答:解:(Ⅰ)由(2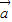 +3
+3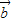 )•(2
)•(2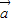 -
-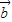 )=61得,4
)=61得,4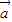 2+4
2+4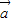 •
•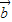 -3
-3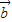 2=61.
2=61.
又|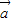 |=4,|
|=4,|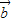 |=3,可得
|=3,可得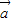 •
•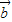 =6. …(4分)
=6. …(4分)
(Ⅱ)设向量 与
与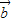 的夹角为θ,
的夹角为θ,
则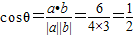 ,
,
可知向量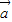 与
与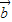 的夹角为60°. …(8分)
的夹角为60°. …(8分)
(Ⅲ)由(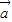 -
-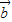 )2=
)2=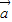 2-2
2-2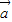 •
•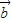 +
+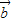 2=13可得,
2=13可得,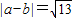 .…(12分)
.…(12分)
点评:本题考查平面向量数量积的运算,解题的关键是熟练掌握数量积的公式及其运算性质,向量的角的数量积表示,本题是数量积运用的基本题型.考查了方程的思想,转化的思想及运算变形的能力.
 +3
+3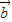 )•(2
)•(2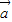 -
-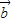 )=61得,4
)=61得,4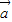 2+4
2+4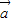 •
•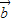 -3
-3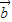 2=61将|
2=61将|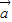 |=4,|
|=4,|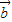 |=3,代入即可求得两向量的内积;
|=3,代入即可求得两向量的内积;(Ⅱ)由公式
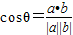 求出向量
求出向量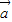 与
与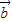 的夹角余弦,再由出对应的角;
的夹角余弦,再由出对应的角;(Ⅲ)先求出(
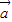 -
-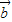 )2=
)2=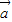 2-2
2-2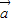 •
•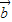 +
+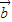 2=13,再开方求出两向量差的模.
2=13,再开方求出两向量差的模.解答:解:(Ⅰ)由(2
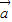 +3
+3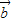 )•(2
)•(2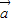 -
-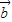 )=61得,4
)=61得,4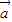 2+4
2+4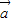 •
•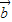 -3
-3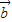 2=61.
2=61.又|
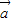 |=4,|
|=4,|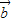 |=3,可得
|=3,可得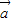 •
•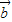 =6. …(4分)
=6. …(4分)(Ⅱ)设向量
 与
与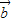 的夹角为θ,
的夹角为θ,则
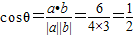 ,
,可知向量
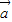 与
与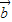 的夹角为60°. …(8分)
的夹角为60°. …(8分)(Ⅲ)由(
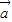 -
-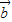 )2=
)2=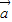 2-2
2-2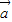 •
•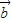 +
+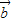 2=13可得,
2=13可得,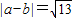 .…(12分)
.…(12分)点评:本题考查平面向量数量积的运算,解题的关键是熟练掌握数量积的公式及其运算性质,向量的角的数量积表示,本题是数量积运用的基本题型.考查了方程的思想,转化的思想及运算变形的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与
与 满足|
满足| |=1,|
|=1,| |=2,且
|=2,且 ⊥(
⊥( +
+ ),则向量
),则向量 与
与 的夹角为 .
的夹角为 . 与
与 满足|
满足| |=1,|
|=1,| |=2,且
|=2,且 ⊥(
⊥( +
+ ),则向量
),则向量 与
与 的夹角为 .
的夹角为 . 与
与 满足|
满足| |=1,|
|=1,| |=2,且
|=2,且 ⊥(
⊥( +
+ ),则向量
),则向量 与
与 的夹角为 .
的夹角为 . 与
与 满足|
满足| |=1,|
|=1,| |=2,且
|=2,且 ⊥(
⊥( +
+ ),则向量
),则向量 与
与 的夹角为 .
的夹角为 .