题目内容
已知函数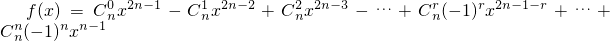 ,n∈N*.
,n∈N*.
(1)当n≥2时,求函数f(x)的极大值和极小值;
(2)是否存在等差数列{an},使得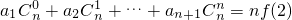 对一切n∈N*都成立?并说明理由.
对一切n∈N*都成立?并说明理由.
解:(1)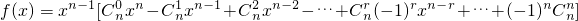 =xn-1(x-1)n,f'(x)=(n-1)xn-2(x-1)n+xn-1•n(x-1)n-1=xn-2(x-1)n-1[(n-1)(x-1)+nx],
=xn-1(x-1)n,f'(x)=(n-1)xn-2(x-1)n+xn-1•n(x-1)n-1=xn-2(x-1)n-1[(n-1)(x-1)+nx],
令f'(x)=0得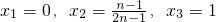 ,
,
因为n≥2,所以x1<x2<x3.…(2分)
当n为偶数时f(x)的增减性如下表:
所以当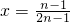 时,
时,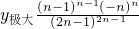 ;当x=1时,y极小=0.…(4分)
;当x=1时,y极小=0.…(4分)
当n为奇数时f(x)的增减性如下表:
所以x=0时,y极大=0;当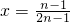 时,
时,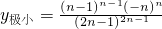 .…(6分)
.…(6分)
(2)假设存在等差数列{an}使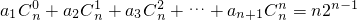 成立,
成立,
由组合数的性质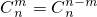 ,
,
把等式变为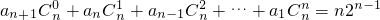 ,
,
两式相加,因为{an}是等差数列,所以a1+an+1=a2+an=a3+an-1=…=an+1+a1,
故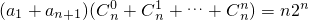 ,
,
所以a1+an+1=n. …(8分)
再分别令n=1,n=2,得a1+a2=1且a1+a3=2,
进一步可得满足题设的等差数列{an}的通项公式为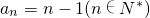 .…(10分)
.…(10分)
分析:(1)先利用二项式定理化简f(x),再求出其导函数f'(x),利用导函数值的正负求出函数的单调区间,进而求出函数f(x)的极大值和极小值;
(2)对于存在性问题,可先假设存在,即假设存在等差数列{an},结合组合数和性质得到a1+an+1=n,再分别令n=1,n=2,得a1+a2=1且a1+a3=2,进一步可得满足题设的等差数列{an}的通项公式,故存在等差数列{bn},满足条件.
点评:本题主要考查二项式定理,等差数列的通项公式,考查利用导数研究函数的极值以及函数的单调性与导数的关系.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,学生应熟练掌握.
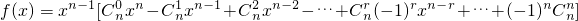 =xn-1(x-1)n,f'(x)=(n-1)xn-2(x-1)n+xn-1•n(x-1)n-1=xn-2(x-1)n-1[(n-1)(x-1)+nx],
=xn-1(x-1)n,f'(x)=(n-1)xn-2(x-1)n+xn-1•n(x-1)n-1=xn-2(x-1)n-1[(n-1)(x-1)+nx],令f'(x)=0得
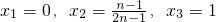 ,
,因为n≥2,所以x1<x2<x3.…(2分)
当n为偶数时f(x)的增减性如下表:
| x | (-∞,0) | 0 |  | 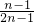 | 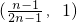 | 1 | (1,+∞) |
| f'(x) | + | 0 | + | 0 | - | 0 | + |
| f(x) | ↗ | 无极值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
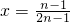 时,
时,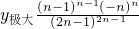 ;当x=1时,y极小=0.…(4分)
;当x=1时,y极小=0.…(4分)当n为奇数时f(x)的增减性如下表:
| x | (-∞,0) | 0 |  | 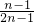 | 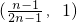 | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ | 无极值 | ↗ |
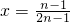 时,
时,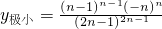 .…(6分)
.…(6分)(2)假设存在等差数列{an}使
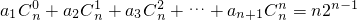 成立,
成立,由组合数的性质
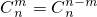 ,
,把等式变为
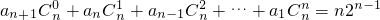 ,
,两式相加,因为{an}是等差数列,所以a1+an+1=a2+an=a3+an-1=…=an+1+a1,
故
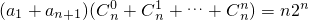 ,
,所以a1+an+1=n. …(8分)
再分别令n=1,n=2,得a1+a2=1且a1+a3=2,
进一步可得满足题设的等差数列{an}的通项公式为
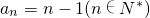 .…(10分)
.…(10分)分析:(1)先利用二项式定理化简f(x),再求出其导函数f'(x),利用导函数值的正负求出函数的单调区间,进而求出函数f(x)的极大值和极小值;
(2)对于存在性问题,可先假设存在,即假设存在等差数列{an},结合组合数和性质得到a1+an+1=n,再分别令n=1,n=2,得a1+a2=1且a1+a3=2,进一步可得满足题设的等差数列{an}的通项公式,故存在等差数列{bn},满足条件.
点评:本题主要考查二项式定理,等差数列的通项公式,考查利用导数研究函数的极值以及函数的单调性与导数的关系.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,学生应熟练掌握.

练习册系列答案
相关题目